Pubblicato il 26 gennaio 2020 su FreeRangeStatistics – Traduzione di Edoardo Salvati
// Ispirato dagli Australian Open 2020, ho deciso di indagare in che modo il sistema di teste di serie e la distribuzione dei giocatori nel tabellone principale incidono sul risultato finale di un torneo. Probabilmente ritornerò sull’argomento, ma l’obiettivo odierno è di analizzare l’impatto dell’assegnazione delle teste di serie sulla probabilità per i più forti di vincere, arrivare in finale, in semifinale o nei quarti di finale.
Metto a confronto i risultati di simulazioni di tornei a eliminazione diretta tra questi giocatori in due tipologie di scenari, da un lato un posizionamento del tutto casuale nel tabellone in assenza di teste di serie, dall’altro l’introduzione di 32 teste di serie come accade nei tornei dello Slam.
L’immagine 1 mostra che la scelta della metodologia determina conseguenze differenti: l’adozione delle teste di serie comporta un aumento concreto della probabilità del migliore di vincere o dei due più forti di arrivare in finale, e ha rilevanza ancora maggiore ai fini della determinazione delle semifinali e dei quarti di finale.
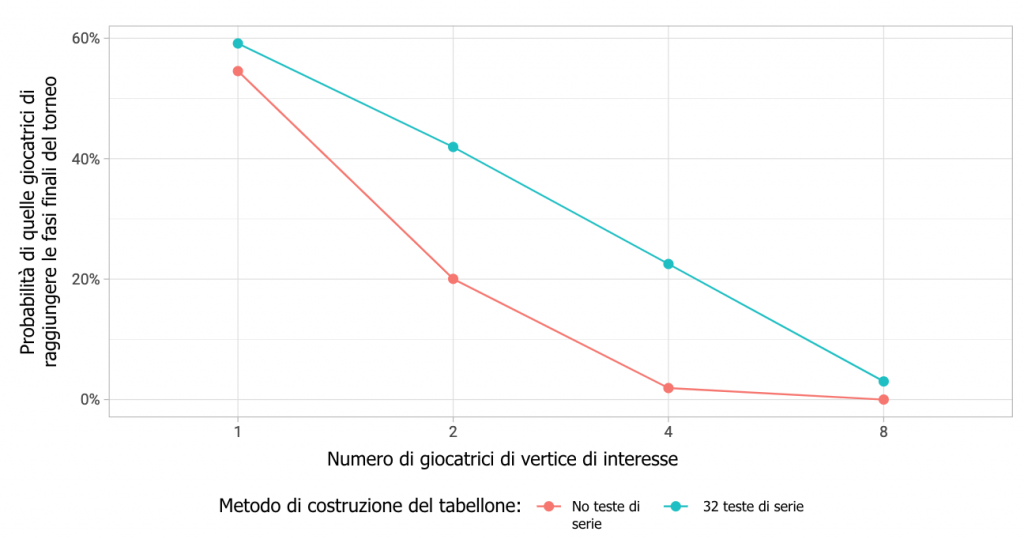
IMMAGINE 1 – Impatto del sistema a teste di serie sul risultato che i migliori possono raggiungere
Distribuzione della bravura dei giocatori
Questo significa che, ad esempio, con 32 giocatori che ricevono una posizione speciale in tabellone grazie alla testa di serie, esiste una probabilità del 22% che in semifinale arriveranno i migliori quattro, rispetto una probabilità di solo il 2% con un tabellone casuale. In una assegnazione casuale, la probabilità di vedere i migliori otto nei quarti di finale è di fatto prossima allo zero, mentre in un tabellone con teste di serie succederà il 3% delle volte (che non è comunque molto spesso, aspetto che però non dovrebbe destare stupore tra coloro che seguono il tennis regolarmente). Di contro, la probabilità che le prime due teste di serie siano in finale è del 42% in un tabellone con teste di serie e solo del 20% in uno casuale.
Va sottolineato che questi risultati dipenderanno dalla distribuzione della bravura dei giocatori nello specifico torneo. All’estremo, se il più forte è in grado di dominare tutti gli altri, la presenza delle teste di serie non farà alcuna differenza per la vittoria finale.
Valori teorici di riferimento
Possiamo calcolare altri valori teorici come limiti di riferimento. Ad esempio, se i primi due giocatori fossero effettivamente invincibili contro chiunque tranne che l’altro, si incontrerebbero in finale il 100% delle volte in un tabellone con teste di serie e il 50% delle volte in un tabellone casuale. Qualsiasi valore inferiore (il 42% e il 20% nel nostro caso) identifica il divario tra un livello “decisamente” alto di questi due giocatori nei confronti degli altri e un livello “infinitamente” alto.
Stephanie Kovalchik ha scritto sulle conseguenze dell’ipotesi di riduzione da 32 a 16 teste di serie negli Slam (che non ha poi avuto seguito), in cui ha mostrato che i risultati sarebbero stati meno esatti rispetto a un sistema a 32 teste di serie, dove per esatto s’intende il raggiungimento del turno atteso da parte del giocatore in funzione della sua classifica.
Serie storica di risultati
Per procedere con l’analisi, ho utilizzato dati sulla bravura effettiva relativa dei giocatori ottenuti grazie al pacchetto {deuce} R codificato da Kovalchik. Mi serviva un intervallo realistico di valori sulla bravura che potessero essere applicati a scontri diretti come in un torneo reale. Ho scelto di concentrarmi su un preciso momento temporale invece di una sfida tra ere che, per esempio, avrebbe messo di fronte Margaret Court e Serena Williams. Onde evitare confusione con l’attualità, ho scelto la stagione femminile del 1990. L’immagine 2 riepiloga le prime 10 a fine 1990 sulla base della loro valutazione Elo.
IMMAGINE 2 – Prime 10 giocatrici per valutazione Elo a fine 1990
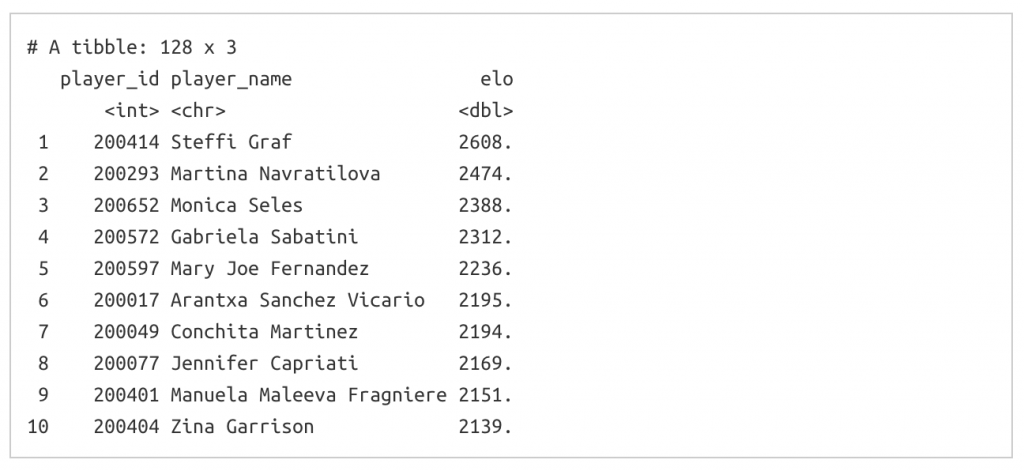
Tramite dati raccolti da Jeff Sackmann, Kovalchik fornisce le valutazioni Elo per ciascuna giocatrice per specifico momento temporale. Avevo già parlato di Elo in merito al Backgammon e al calcio australiano. Si tratta di un metodo molto efficace per fare valutazioni di giocatori rispetto all’effettivo rendimento, con il grande vantaggio di poterne derivare probabilità per un qualsiasi ipotetico scontro diretto.
La valutazione è oggetto di aggiustamenti incrementali in funzione della rispondenza tra situazione effettiva e probabilità derivate dalle valutazione Elo alla vigilia della partita. Questo ne fa un’indice utile e con capacità di correzione automatica, e facilmente integrabile in un modello statistico.
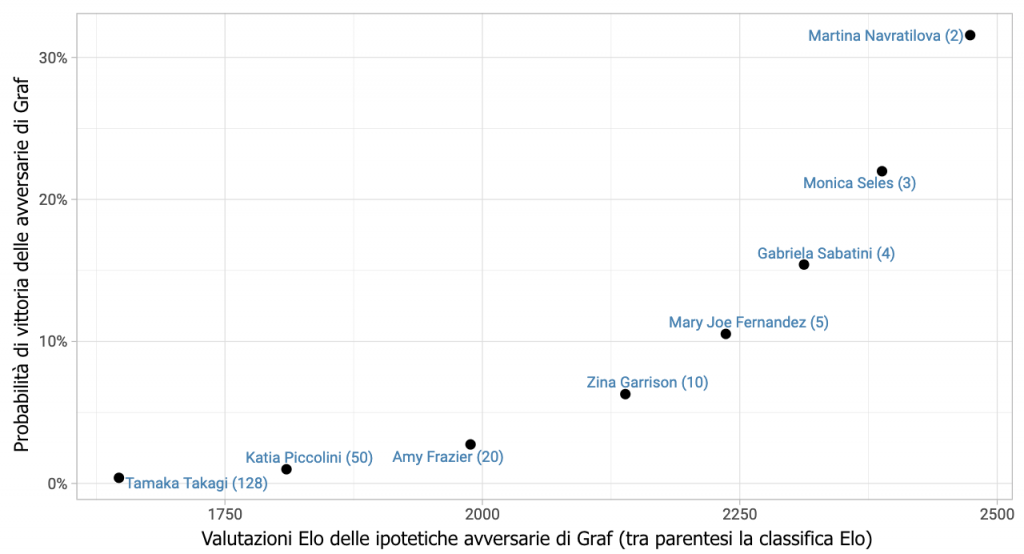
Per essere sicuro della corretta conversione delle valutazioni Elo di Kovalchik in probabilità, mi affido alla sua funzione elo_prediction() per la stima della probabilità di vittoria in ciascun accoppiamento. L’immagine 3 illustra mostra la probabilità di battere Steffi Graf da parte di una selezione di giocatrici classificate tra la posizione 2 e la 128 in termini di valutazioni Elo (Graf che, dall’inizio dell’era Open, è la giocatrice che la più alta valutazione assoluta).
IMMAGINE 3 – Probabilità di alcune tra le prime 128 di battere Graf alla fine del 1990
La simulazione dei tabelloni e risultati
Per completare la laboriosa attività di simulazione di tornei tra queste 128 giocatrici, ho scritto una funzione simulate_tournament() il cui principale argomento è una struttura dati di 128 righe di fila che rappresentano il tabellone, come nell’immagine 4.
IMMAGINE 4 – Funzione simulate_tournament()
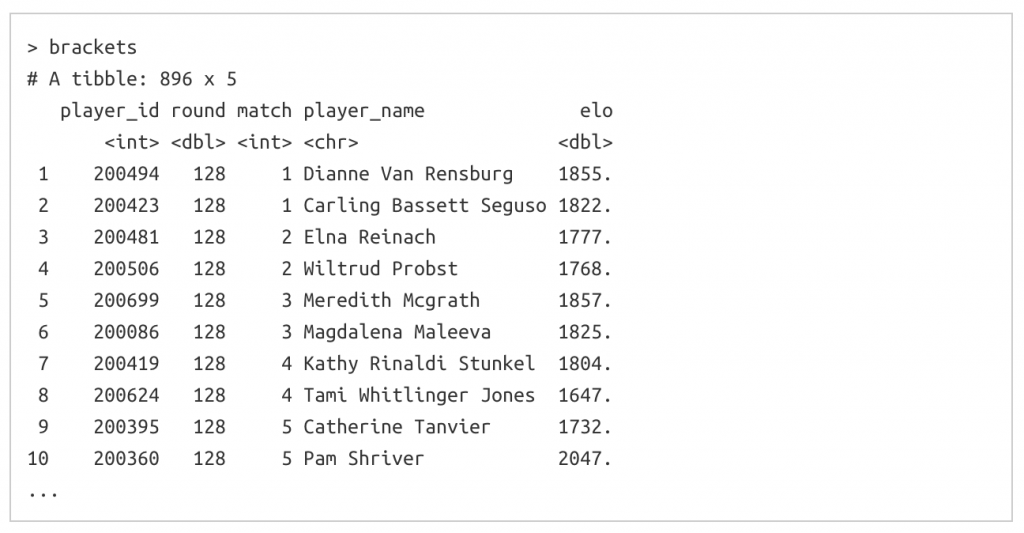
Questo indica ad esempio che nel primo turno giocato (“round of 128”) Dianne Van Rensburg giocherà contro Carling Basset Seguso nella partita 1 (match 1). L’immagine 5 mostra il risultato filtrando per la partita 1 del secondo turno (“round of 64”)
IMMAGINE 5 – Partite del secondo turno della simulazione

Troviamo quattro giocatrici nella partita 1. Però una tra Van Resnburg e Seguso avrà perso nel primo turno, così come una tra Elna Reinach e Wiltrud Probst. Con un po’ di attenzione, l’oggetto brackets riesce a contenere l’intero tabellone principale, e può essere disegnato in modo che le prime 32 teste di serie siano allocate nei singoli quarti come richiesto da un tabellone a 32 teste di serie. Il resto del codice che ho scritto esegue questa simulazione per i due scenari di tabellone che ho individuato in precedenza.
Arriviamo ai risultati
La tabella riepiloga la distribuzione delle vincitrici. Non sorprende che Graf vinca più simulazioni di torneo di qualsiasi altra, 5454 su 10.000 con un tabellone casuale, e 5913 su 10.000 con un tabellone a 32 teste di serie. Anche in un periodo di dominio totale di Graf, ci sono comunque giocatrici (e non solo alcune tra quelle di vertice) con una probabilità di vittoria diversa da zero. Ed è questo che attrae le persone a seguire il tennis. È interessante come da Monica Seles (a quel tempo al terzo posto delle valutazioni Elo) a scendere, è più probabile che una giocatrice vinca il torneo simulato in un tabellone casuale invece che in uno con le teste di serie.
Vincitrice Class. No t.d.s. 32 t.d.s. Graf 1 5454 5913 Navratilova 2 2089 2219 Seles 3 1064 1018 Sabatini 4 510 418 M.J. Fernandez 5 213 132 Martinez 7 110 66 Sanchez Vicario 6 113 63 Capriati 8 89 42 Maleeva Fragniere 9 66 34 Garrison 10 58 26
Questo rimanda ai risultati evidenziati dal grafico dell’immagine 1 di inizio articolo. Spero presto di riprendere questa tematica e confrontare i due metodi con l’alternativa proposta da Charles Dodgson in “Lawn Tennis Tournaments. The True Method of Assigning Prizes with a Proof of the Fallacy of the Present Method”. Dodgson, che oltre a essere un matematico e logico trovò il tempo di dare vita a uno dei più importanti personaggi della letteratura inglese (in Alice nel paese delle meraviglie con lo pseudonimo di Lewis Carrol, n.d.t.), scriveva prima della diffusione del concetto di teste di serie. Propose un’alternativa al torneo a eliminazione diretta che a suo dire garantiva l’assegnazione esatta dei primi tre premi ai tre giocatori più forti. Il suo ragionamento però poggiava su una visione non probabilistica del significato di migliore. Certamente meritevole di approfondimento, ma per un’altra occasione. ◼︎