Pubblicato il 20 aprile 2018 su HiddenGameOfTennis – Traduzione di Edoardo Salvati
// Gli errori non forzati sono comunemente associati all’idea che un giocatore stia “tirando troppo”, anche se è indubbio che comprendano errori non dettati dall’aggressività. Qualsiasi professionista con l’obiettivo di un gioco più offensivo deve chiedersi quale sia la sua avversione al rischio nel ricercare vincenti e nel forzare gli avversari all’errore.
Grazie ai dati del Match Charting Project, ho analizzato la tematica nell’ambito del circuito femminile. Ho fatto questa scelta principalmente perché si sente spesso dire che le giocatrici devono essere più aggressive, e anche perché sapevo di non dovermi preoccupare delle partite al meglio dei cinque set.
Offensività nel gioco femminile
Ho iniziato restringendo il campo alle partite dopo il 2006, l’anno in cui ritengo che i cambiamenti nei materiali di corde e racchette abbiano maggiormente inciso sullo stile di gioco. Con questo non voglio dire che è proprio il 2006 da cui tutto non è stato più lo stesso, ma è anche il riferimento prima del quale la maggior parte delle giocatrici ora attive sul circuito non aveva un numero significativo di partite valide per i criteri dell’analisi. Mi è sembrato quindi un buon punto di partenza.
Sono emerse 1528 partite, che equivalgono a 3056 partite-giocatrice.
Subito alcune statistiche descrittive che riguardano l’insieme completo delle 3056 partite-giocatrice. Il numero medio di vincenti, errori forzati ed errori non forzati è rispettivamente di 20.6, 20.5 e 27.6.
Dovremmo essere in grado di ipotizzare che il numero effettivo di vincenti non sia strettamente correlato con la vittoria (o la sconfitta) della partita, e lo stesso per gli errori forzati e non forzati. I dati lo confermano, con una correlazione positiva molto debole di .22 e di .19 per il numero di errori forzati, e una correlazione negativa debole di -.28 per il numero di errori non forzati. Per questo motivo, mi concentrerò sugli indici invece che contare le statistiche.
Indici e correlazioni
Ho considerato due indici rilevanti ai fini di quest’analisi: (a) il rapporto tra vincenti (V) su errori non forzati (EF) espresso come V/ENF e (b) il rapporto tra vincenti + errori forzati su errori non forzati (ENF) espresso come (V + EF)/ENF. Si ottengono ovviamente correlazioni migliori rispetto al conteggio statistico, ma non sono comunque decisive. L’indice V/ENF ha una correlazione di .44 e l’indice (V + EF)/ENF ha sorprendentemente – almeno per me – una correlazione solo di .40.
Il significato di tutto questo è che vincere una partita di tennis ha ben più a che vedere della semplice valutazione dei vincenti, degli errori non forzati e di quelli forzati, primo fra tutti ad esempio il momento della partita in cui si verificano. In ogni caso, una correlazione positiva di .44 è indicazione che l’indice V/ENF è meritevole di approfondimento.
Visto che l’obiettivo è stabilire se una giocatrice sta forzando la mano nella ricerca del gioco offensivo, non c’è ragione di considerare anche quelle partite con un numero totale ridotto di errori non forzati. Sono partite caratterizzate da un approccio super conservativo che si traduce in pochi vincenti o partite in cui uno stato di forma impeccabile consente a una giocatrice di non dover fare scelte complicate in termini di aggressività in campo.
Su questa linea, ho ulteriormente ristretto il campione alle sole partite in cui una delle due giocatrici ha commesso almeno 25 errori non forzati che, in partite che terminano in due set, sono molti. Non lo sono in partite andate al terzo set, ma è comunque un rendimento eccessivamente negativo.
A meno di non riuscire proprio a tenere la palla in campo, 25 errori non forzati sono una prima indicazione della volontà di avere un gioco più offensivo. È di poco inferiore al numero medio di errori non forzati per giocatrice-partita nel campione, ma è vicino al valore mediano di 26.
La ricerca del punto di pareggio
Raggiunto l’insieme ideale di partite, ho analizzato il rapporto V/ENF alla ricerca di un punto di pareggio superato il quale una giocatrice ha più probabilità di vincere che di perdere.
Ho quindi eseguito una regressione logistica per calcolare la probabilità di vincere la partita con l’indice V/ENF come unica variabile. Ci sono diversi strumenti per calcolare una regressione logistica (come R, Python, etc), ma per un risultato semplice e diretto preferisco usare l’algoritmo di calcolo messo a disposizione da statpages.
Il punto dal quale la vittoria diventa più probabile è un indice di .84 vincenti su errori non forzati. In presenza di 30 errori non forzati, si vogliono almeno 25 vincenti in modo da andare a pareggio al 50%.
L’immagine 1 mostra la rappresentazione grafica di questo concetto.
IMMAGINE 1 – Funzione logaritmica dell’indice V/ENF
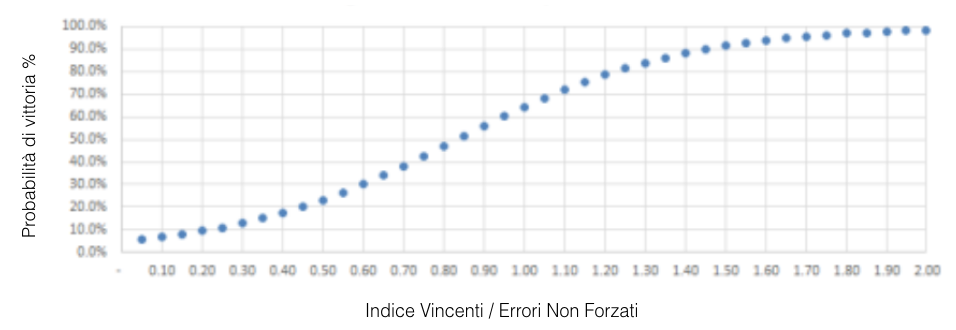
Il tradizionale adagio del tennis di non trovarsi con un numero di vincenti inferiore agli errori non forzati è messo in ottima luce da quest’analisi. Se una giocatrice è in grado di compensare i molti errori che commette con un analogo numero di vincenti, la sua percentuale di vittoria attesa è di circa il 64%.
Naturalmente, si dovrebbe evitare di avere come obiettivo il 50% di probabilità di vittoria, perché passare da un 49.9% a un 50.1% non garantisce troppa sicurezza su un esito finale positivo. E questo è ancora più vero considerando l’incertezza intrinseca associata a qualsiasi pronostico basato sulle probabilità.
Per lasciare del margine nella gestione di queste problematiche, ho convenuto che una probabilità del 57.5% fosse un’obiettivo più ragionevole, in modo da tenere conto di parte dell’incertezza intrinseca ma discostandosi contestualmente da quelle partite molto equilibrate e aperte a un risultato finale a favore di una o dell’altra giocatrice (con probabilità dal 47% al 53%).
Al 57.5% di probabilità di vittoria, l’indice V/ENF è intorno a .92, vale a dire che se si ha una passività di 30 errori non forzati si cercano almeno 28 vincenti che li giustifichino. Non troppo lontano dalla tradizione, ma con un po’ di spazio di manovra.
Non si può tralasciare il rendimento dell’avversaria
L’obiettivo del .92 è però fuorviante, perché ignora il rendimento dell’avversaria. Si possono avere 28 vincenti e 30 errori non forzati, con una probabilità di vittoria attesa del 57.5%. È possibile però che anche l’avversaria commetta molti errori e il suo indice sia più alto. Oppure, che l’avversaria commetta molti meno errori.
Esaminiamo solamente le partite nelle quali anche l’avversaria ha fatto almeno 25 errori. Per questo sottoinsieme, ipotizziamo che la giocatrice in esame stia avendo un rendimento discreto con una probabilità di vittoria di almeno il 40%, sulla base del suo indice V/ENF (di circa .70), ma non può essere considerata la favorita indiscussa semplicemente in funzione del livello di gioco, cioè quindi meno del 68% di probabilità di vittoria (o un indice V/ENF di circa 1.05). Ci sono 172 partite di questo tipo nel campione considerato.
In esse, il valore medio dell’indice è di .85, e il modello logaritmico prevede una probabilità di vittoria del 51.3%. Le giocatrici in esame hanno in realtà vinto 114 delle 172 partite con una percentuale molto più alta.
Però, il rendimento delle avversarie non è equamente distribuito. Le giocatrici in esame hanno avuto un indice migliore nella grande maggioranza delle partite (117 su 172) e in 95 delle 114 vittorie. La giocatrice in esame ha vinto 19 volte e perso 36 quando l’avversaria ha avuto un indice superiore.
Se spingiamo ora l’indice della giocatrice in esame ad almeno .85, il valore in cui abbiamo detto essere leggermente favorita, e lo portiamo poi al valore 1.05, otteniamo solo 85 partite, di cui 20 con un indice migliore da parte dell’avversaria. La giocatrice in esame ha vinto 8 di quelle 20 partite, ma ne ha vinte 54 su 65 quando il suo indice è stato più alto. Non sorprende quindi che il gioco dell’avversaria rivesta importanza nella ricerca del punto di equilibrio tra vincenti ed errori non forzati.
Le situazioni di gioco con pochi errori
Occupiamoci dell’altra circostanza, quella in cui non vengono commessi molti errori. Cosa succede se escludiamo tutte le partite in cui entrambe le giocatrici hanno fatto almeno 25 errori non forzati, lasciando quelle in cui invece solo una giocatrice ne ha commessi almeno 25?
Il campione complessivo si riduce del 40%, che è già un’indicazione interessante di per sé, come se gli errori non forzati da un lato della rete generassero errori non forzati dall’altro.
Tralasciando questa considerazione, mi aspetto che in un campione di partite senza avversarie che commettono molti errori non forzati debba esserci un numero ancora più alto di vincenti per la giocatrice in esame che compensino i suoi errori non forzati, se vuole effettivamente vincere la partita.
L’immagine 2 mostra la sovrapposizione tra il grafico del modello che considera solo le partite con una giocatrice prona all’errore (in rosso) e il grafico del modello che include anche le partite in cui entrambe le giocatrici hanno commesso almeno 25 errori (in blu).
IMMAGINE 2 – Funzione logaritmica dell’indice V/ENF per due modelli a confronto
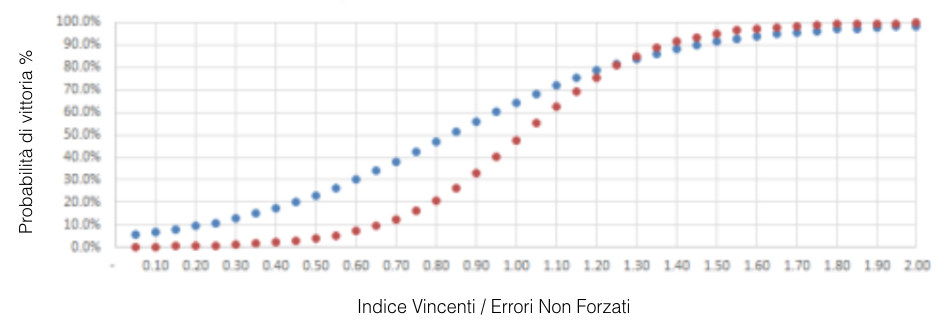
In questo sottoinsieme di partite, serve avere un numero di vincenti in rapporto di 1:1 con gli errori non forzati anche solo per avvicinarsi a una probabilità di vittoria in zona positiva, appena inferiore al 50%. Vale la pena ricordare che con il campione di dati originario in presenza di un rapporto di 1:1 la probabilità di vittoria era del 64%.
Sempre in questo insieme ristretto, per raggiungere l’obiettivo del 57.5% di probabilità di vittoria inizialmente stabilito, serve il 7% di vincenti in più degli errori non forzati se l’avversaria ha meno di 25 errori non forzati. Se la giocatrice in esame ha 30 errori non forzati, si tratta in sostanza di 4 vincenti in più (il 15%) di quelli necessari con il campione di partite più ampio.
****
Vorrei sottolineare che non si può prevedere l’esito di una partita solamente sulla base del rapporto tra vincenti ed errori non forzati nelle due forme viste in precedenza, perché sono indicative di determinati aspetti, ma non di tutti quelli che intervengono nel corso di una partita.
Fatta questa premessa, ci sono un paio di elementi particolarmente interessanti. Da un lato, giocatrici aggressive che non riescono a evitare errori non forzati possono in effetti fare leva sul tradizionale adagio del rapporto di 1:1 tra vincenti ed errori non forzati come parametro approssimativo di vittoria finale. Farlo contro avversarie simili può portare immediatamente a una probabilità positiva di vittoria, specie se eseguito con più efficacia.
Al contrario, l’idea di poter attuare una strategia così rischiosa e cavarsela contro un’avversaria che commette molti meno errori è di dubbia validità. Si sente spesso dire che le giocatrici devono “continuare a essere offensive” anche contro avversarie più difensive.
Le giocatrici stesse affermano di scendere in campo cercando di imporre il proprio gioco. Ma se questo significa che per riuscire a essere offensiva a una giocatrice serve incamerare molti errori non forzati, allora deve poi rendersi conto che il margine tra vincenti ed errori non forzati è – contro determinate avversarie – più ristretto o magari anche invertito. A un certo punto, la strategia dovrà essere adattata al gioco espresso dall’avversaria.
Non ho analizzato il rapporto tra vincenti + errori forzati su errori non forzati (ENF) espresso come (V + EF)/ENF che ho indicato al punto (b). È un indice intuitivamente interessante, perché si presuppone che una giocatrice rischi più errori non forzati non solo cercando dei vincenti, ma anche per indurre l’avversaria all’errore.
Però, l’indice (V + EF)/ENF ha una correlazione inferiore con la vittoria finale di V/ENF, almeno nel campione utilizzato. Se dovessi scegliere (come il poco tempo mi ha costretto a fare), prenderei l’indice a più alta correlazione. Analizzerò l’indice (V + EF)/ENF in futuro se ci sarà occasione.
La percezione del numero di vincenti ed errori non forzati
Tuttavia, ha contribuito alla scelta il fatto che, dal punto di vista della giocatrice che valuta se apportare modifiche al suo gioco durante la partita, è più facile mentalmente separare vincenti da errori non forzati di quanto non lo sia tenere nota degli errori forzati dell’avversaria rispetto ai colpi che avrebbe dovuto rimandare in campo ma che non è stata capace di fare.
I due terzi dei valori che l’indice V/ENF assume nel campione sono tra il .5 e l’1, quindi una giocatrice dovrebbe avere percezione se vincenti ed errori non forzati sono all’incirca uguali o se prevalgono i secondi.
Al contrario, i due terzi dei valori che l’indice (V+EF)/ENF assume sono tra il .9 e l’1.75, quindi oltre a essere più complicati da tenere a mente, è probabile che una giocatrice abbia più difficoltà a stabilirne il rapporto se vengono aggiunti anche gli errori forzati. ◼︎


