Pubblicato il 26 maggio 2018 su HiddenGameOfTennis – Traduzione di Edoardo Salvati
// Stavo esercitando le mie conoscenze di Python Pandas – che da zero sono salite all’infinitesimo incremento di zero previsto dalla scala con cui si misurano le suddette – su alcuni dati punto per punto dal database del Match Charting Project e mi è venuta la curiosità di scoprire quanto siano frequenti gli scambi incrociati di dritto e quelli di rovescio nel tennis maschile.
Ho fatto partire il campione dei dati dal 2006 (fino a circa febbraio 2018), ottenendo un sottoinsieme di quasi 242 mila colpi. La tabella mostra il numero di scambi incrociati di dritto e di rovescio, suddivisi per numero di colpi che compongono lo scambio incrociato (la risposta al servizio non è conteggiata). Il numero in alto a sinistra (101,700) si riferisce agli scambi del sottoinsieme fatti da almeno tre colpi (a seguito della risposta) e le percentuali sono calcolate in funzione.
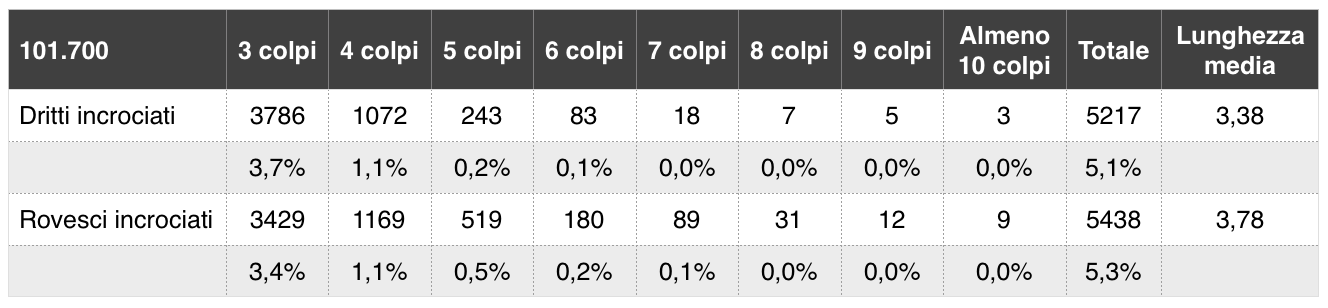
Più scambi incrociati di rovescio che di dritto
Mi ha sorpreso trovare che, tra gli uomini, ci siano scambi incrociati di rovescio in misura maggiore, seppur di poco, di quelli di dritto. Va specificato che ho escluso scambi con colpi tagliati.
Se per il dritto è irrilevante (ne ho trovati solo due che, francamente, direi che sono due di troppo, e in entrambi uno dei giocatori era Stanislas Wawrinka), per il rovescio sono rimasti fuori dalla tabella 374 scambi.
In media, gli scambi di rovescio sono leggermente più lunghi, con il 93% degli scambi incrociati di dritto che terminano al quarto colpo e solo l’85% di quelli con il rovescio, forse perché i giocatori hanno più facilità a cambiare sul lato del dritto o perché il dritto è un colpo molto più efficace per terminare lo scambio con un vincente.
Anche se sembra che circa il 10% degli scambi (e circa il 4% di tutti i punti) includa una sequenza di almeno tre colpi incrociati, sono in realtà di meno, perché alcuni dei punti considerati hanno al loro interno due o più occorrenze con uno scambio di almeno 3 incrociati.
Ad esempio, uno scambio composto da tre dritti incrociati, seguito da un dritto lungolinea, poi altri tre dritti incrociati e un rovescio lungolinea, produce in totale 3 occorrenze valide per la tabella a fronte di un solo punto (nella codifica del Match Charting Project lo scambio è rappresentato con f1f1f1f3b3b3b3b1f1f1f1. Sono sicuro che con questo vi ho proprio ingolosito, non è così?).
Ipotesi di tipo gioco sugli scambi incrociati
Ho ipotizzato che il giocatore che colpisce il secondo colpo di uno scambio incrociato di almeno tre colpi è anche colui che più probabilmente deciderà di interromperlo. Ho pensato cioè che il secondo giocatore non voglia rimanere in una situazione di gioco che ha iniziato l’avversario, e non diventa davvero una situazione fino a che il primo giocatore non colpisce il terzo colpo.
Funziona così: il giocatore che colpisce il primo colpo ha giocato semplicemente un colpo, ma quando arriva dal suo lato di campo un colpo incrociato, pensa tra sé “Forse è un buon momento per imporre il mio gioco e bloccare l’avversario in uno scambio come questo, per poi interromperlo e vincerlo”. Al momento di colpire il quarto colpo, l’avversario pensa tra sé “Non mi farò certamente incastrare in uno scambio incrociato, me ne tiro fuori!”.
È un’ipotesi praticamente inevitabile, visto che gli scambi incrociati da tre colpi sono i più frequenti: il secondo colpo del giocatore che ha colpito per secondo è quello che più spesso interrompe questa particolare situazione.
Cosa succede se eliminiamo gli scambi da tre colpi (cioè più della metà degli scambi incrociati)? È quattro volte più probabile che il giocatore che inizia lo scambio lo interrompa dal lato del dritto e due volte più probabile che lo interrompa dal lato del rovescio.
Se vi capita di guardare le partite del singolare maschile del Roland Garros, provate a osservare quanti scambi incrociati riuscite a individuare e prendete nota di quale dei due giocatori lo interrompe. Fate attenzione anche a vedere se chi interrompe lo scambio incrociato vince poi il punto, perché l’altra mia ipotesi è che vada esattamente così. ◼︎


