Pubblicato il 16 agosto 2021 su StatsOnTheT – Traduzione di Edoardo Salvati
// Con sette partite del tabellone principale a separare un professionista dalla vittoria di uno Slam, sembra quasi ovvio che la continuità di rendimento è essenziale per raggiungere quel risultato. Non esistono giocatori però capaci di giocare al massimo in ogni singola partita. E, soprattutto, nessuno riesce a evitare l’occasionale giornata negativa. Si apre quindi un’interessante domanda, la cui risposta è molto meno ovvia: quale livello di continuità è necessario mantenere per vincere uno Slam?
Si parla spesso, nelle conversazioni di tennis, della continuità di un giocatore come caratteristica che identifica l’abilità nel produrre un rendimento simile da partita a partita, nel bene o nel male. Sono sicura che qualsiasi appassionato citerebbe al volo una manciata di giocatori “poco continui” (ad esempio Gael Monfils, Fabio Fognini e Nick Kyrgios). L’elenco di chi mostra continuità invece non genera alcun dubbio, con la carriera di ognuno dei Grandi Tre definita dalla maestria nella continuità.
Abbiamo tutti una chiara idea del significato di continuità nel tennis e del fatto che sia un tratto importante per un campione, eppure è uno di quegli aspetti che non ci dilunghiamo a quantificare. Ed è un peccato perché non dovrebbe essere così difficile trovare indicatori che, ragionevolmente, danno una misura della continuità. Prendiamo l’immagine 1 e ipotizziamo di avere il rendimento al servizio su un asse e quello alla risposta sull’altro asse. I due giocatori considerati hanno lo stesso obiettivo al servizio e alla risposta, identificato dal cerchio rosso. In media, entrambi riescono a centrare il bersaglio, ma il giocatore sulla sinistra è molto più continuo.
IMMAGINE 1 – Una dimostrazione di differenza di continuità
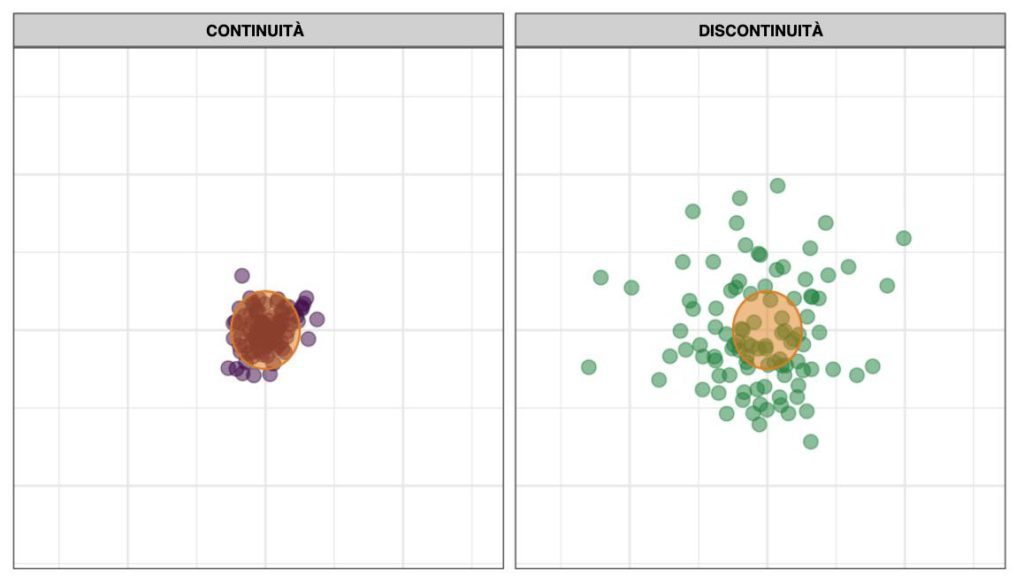
Questa semplice immagine sottolinea come la continuità vada di pari passo con la variazione. Meglio ancora, la continuità è esattamente l’inverso della varianza. Maggiore l’oscillazione nel rendimento di un giocatore, che non può essere attribuita a causa già nota, meno continuo è quel giocatore. Non mancano nomi da elencare oggetto di una conversazione sulla continuità (o sulla sua mancanza). Tra le donne, una giocatrice che penso sia un caso interessante sull’argomento è Aryna Sabalenka.
Attualmente numero 2 del mondo, Sabalenka ha vinto 10 titoli del circuito maggiore in carriera, eppure solo recentemente ha ottenuto i risultati migliori negli Slam, con due semifinali perse prima a Wimbledon e poi agli US Open. Da tempo il suo nome è associato alla possibile vittoria di uno Slam, specialmente dal 2018 quando è entrata tra le prime 15 della classifica ufficiale e tra le prime 10 delle valutazioni Elo. Considerate le aspettative riposte su di lei negli ultimi anni, il fatto che non sia andata oltre due semifinali Slam e non più del quarto turno in Australia e del terzo turno al Roland Garros rappresenta una delusione, e motivo sufficiente per chiedersi come mai Sabalenka, almeno negli Slam, non abbia ancora espresso tutto il suo potenziale.
Alto rischio, alto rendimento
Siamo di fronte a una tipica giocatrice da alto rischio-alto rendimento. Quando è in giornata, il peso dei suoi colpi è in grado di sovrastare qualsiasi altra giocatrice. Quando invece le cose non girano, non sarebbe sorprendente vederla subire un 6-0 da un’avversaria ben più debole. Il limite dei punti di forza di Sabalenka risiede nell’incredibile difficoltà di proporre un tipo di tennis a così bassa percentuale realizzativa. Se si aggiunge la casualità intrinseca di un formato al meglio dei tre set, si ottiene la ricetta da manuale della discontinuità di rendimento. Forse però sto affrettando conclusioni: si può sostenere la tesi che Sabalenka è effettivamente una giocatrice ad alta-varianza?
Per trovare una risposta, possiamo concentrarci su una delle statistiche più rilevanti per la vittoria di una partita, vale a dire la probabilità di vincere un punto al servizio. Una caratteristica della discontinuità di una giocatrice è un’alta variazione partita su partita dei punti vinti al servizio, come facilmente intuibile. La complicazione è data dal fatto che, in una partita, non si osserva la vera probabilità di punti vinti al servizio, ma la percentuale di punti vinti al servizio contro una determinata avversaria, che ovviamente, grazie alla sua bravura alla risposta, incide sul rendimento al servizio. Bisogna quindi tenerne conto, almeno in misura minima.
La formula che segue definisce un modello di regressione di base per ottenere un reale rendimento al servizio:
g(A[Servizio]ij) = β0 + β1(log(Elo)i +log(Elo)j) + β2(log(Elo)i − log(Elo)j)
dove g(A[Servizio]ij) è una funzione logit della percentuale di punti al servizio della giocatrice i contro la giocatrice j. Modelliamo le probabilità log come una funzione lineare della somma tra le valutazioni Elo delle due giocatrici (su scala log) e la differenza nelle loro valutazioni Elo (su scala log). Possiamo ora osservare il rendimento corretto per le attese:
Rij = Yij − A[Serve]ij.
Si tratta semplicemente del valore residuo della percentuale effettiva di punti vinti al servizio contro la percentuale attesa. Altri elementi possono, senza dubbio, spiegare il rendimento al servizio, ma così facendo si riesce a escludere l’effetto avversaria nella variazione partita su partita. L’immagine 2 mostra la densità di questi valori residui per la partite di Sabalenka dal 2019 al 2021, centrata rispetto a una percentuale fissa del 60% di punti vinti al servizio in ogni anno. Emergono differenze anno per anno, ma per tutti gli anni osserviamo molteplici risultati che si discostano dalla media di più del 10%, sia verso l’alto che verso il basso. Ancora più interessante, c’è una maggiore deviazione nel 2021, con la parte alta del suo rendimento che sale anche fino al 20% sopra la media.
IMMAGINE 2 – Il rendimento al servizio di Sabalenka corretto per avversaria, fissato al 60% (la sua percentuale attesa di punti vinti contro una giocatrice di vertice)
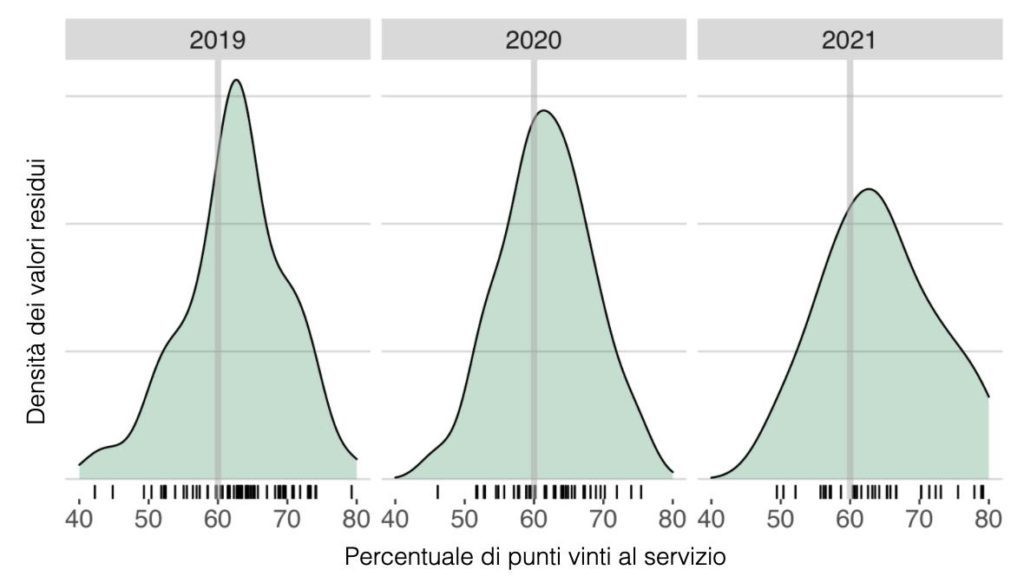
Ci orientiamo su rendimenti al servizio che possono essere in un intorno compreso tra il 20 al 30%, che sembra importante. Lo è davvero? Prendiamo a confronto un’altra giocatrice di assoluta fattura come Ashleigh Barty. Si notano immediatamente densità ben più ridotte per Barty, con in particolare gli anni 2020 e 2021 in cui l’intervallo di oscillazione è più vicino al 10%.
IMMAGINE 3 – Il rendimento al servizio di Barty corretto per avversaria, fissato al 60% (la sua percentuale attesa di punti vinti contro una giocatrice di vertice)
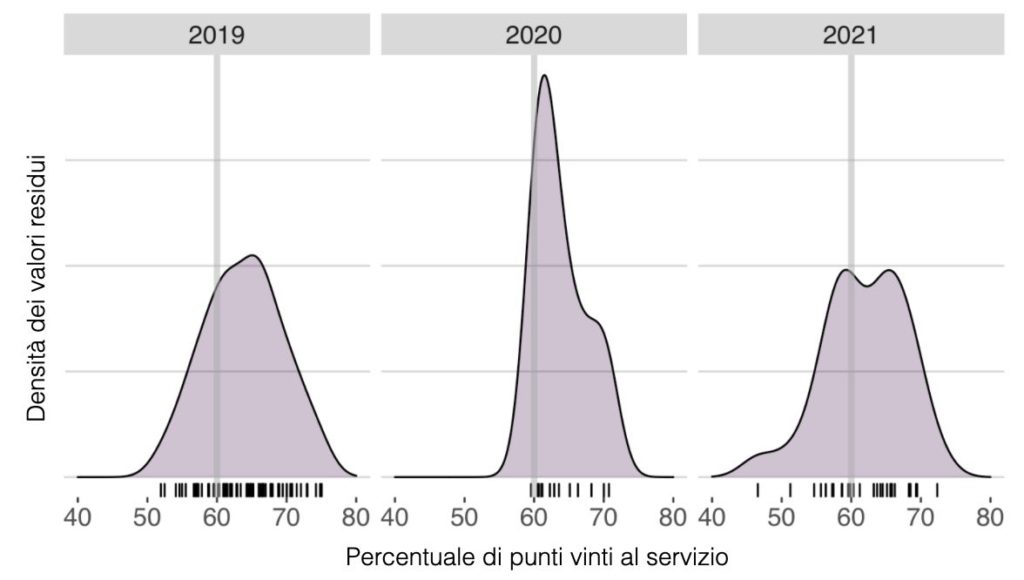
Voglio ora considerare di quanto il livello di variazione osservato nel rendimento al servizio di Sabalenka aumenta la difficoltà nel vittoria del titolo.
Sappiamo che l’esito di un punto nel tennis è strettamente correlato alla bravura al servizio della giocatrice. Da questo assunto, possiamo procedere con una simulazione di torneo Slam al meglio dei tre set per provare a isolare che tipo di incidenza abbia una modifica della variazione nel servizio di Sabalenka sulla sua probabilità di vincere il titolo.
La simulazione di torneo Slam
Per ogni partita su sette turni:
- Primo: derivare p0, la probabilità di tenere il servizio dell’avversaria da una distribuzione a bassa varianza con una media del 55%
- Secondo: derivare p1, la probabilità di tenere il servizio per Sabalenka da una distribuzione con media del 60% e varianza in funzione delle condizioni di continuità
- Terzo: eseguire una simulazione di partita date le probabilità (p0, p1) e determinare la vincitrice
- Si ripetono poi i primi tre passaggi per un milione di volte così da ottenere una distribuzione del risultato delle partite di uno Slam rispetto alle condizioni di continuità definite.
Se si ipotizza che le avversarie di ciascun turno siano della stessa bravura, non si riflette in realtà la difficoltà incrementale associata al fatto che la giocatrice del turno successivo è normalmente più forte. Di conseguenza, la probabilità assoluta di vittoria non è una buona stima del caso reale, ma questo tipo di semplificazione non impedisce comunque di vedere come un aumento della variazione nella prestazione di turno in turno renda sette partite consecutive relativamente più difficili.
Quali sono le condizioni di continuità considerate?
In totale ne ho selezionate dieci, e a questo riguardo l’immagine 5 mostra le distribuzioni della probabilità di rendimento al servizio. I colori indicano la mancanza di continuità espressa come frequenza con cui la probabilità di tenere il servizio si discosta di più di 2 punti percentuali dalla media. È un valore un po’ arbitrario ma di più facile intuizione del concetto di deviazione standard. Nel caso di maggiore continuità, il 40% della percentuale di vittoria al servizio è fuori da questo intervallo, mentre in presenza di maggiore discontinuità il 97% dei casi si posiziona a più di 2 punti percentuali dalla media.
IMMAGINE 4 – Condizioni di continuità usate per valutare il rendimento al servizio di Sabalenka in una simulazione di torneo Slam
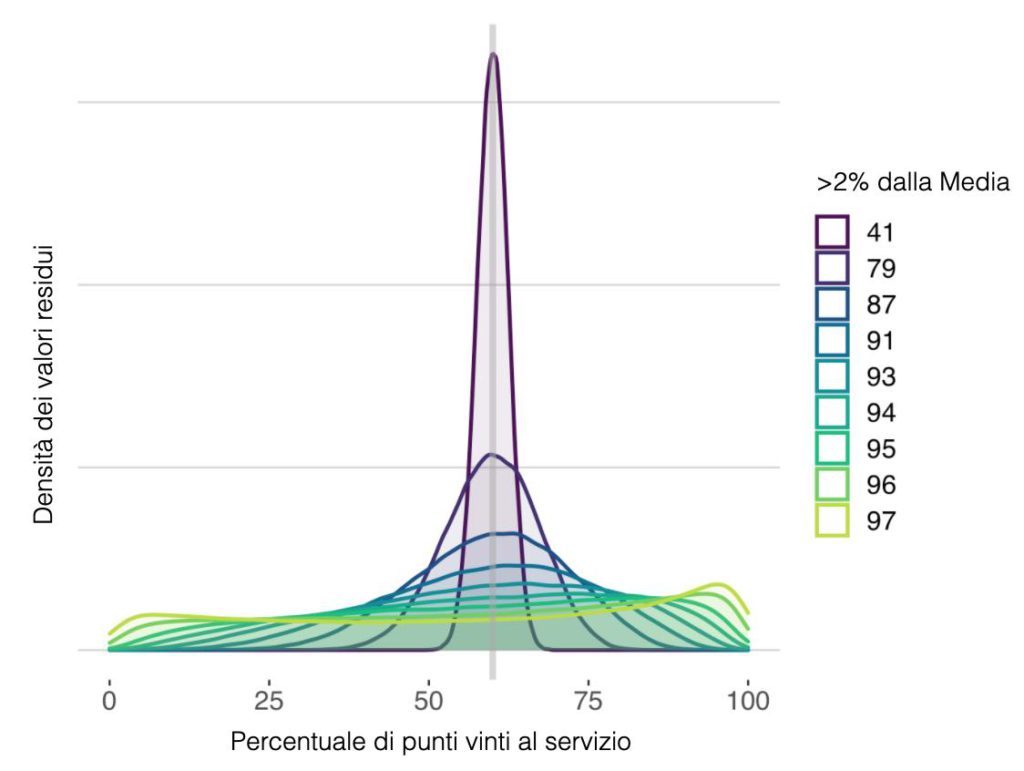
Tiriamo le somme
Partendo dall’idea di un titolo Slam e dalla vittoria di sette partite di fila necessarie, osserviamo un chiaro effetto negativo associato alla mancanza di continuità. Anzi, in termini di intervallo del 2%, si nota una diminuzione verticale una volta che più del 70% delle prestazioni al servizio è a più di due punti percentuali dalla media. Rispetto alla deviazione standard sul rendimento, le probabilità di vincere il torneo si comportano abbastanza linearmente e osserviamo una diminuzione di circa il 2% ogni cinque punti percentuali di aumento della deviazione standard. C’è un effetto simile anche per 5 e 6 partite consecutive vinte, sebbene la percentuale complessiva di vittoria è ovviamente più alta per ogni condizione.
IMMAGINE 5 – Confronto di variazione nelle probabilità di vittoria di Sabalenka in termini di intervallo del 2% e di deviazione standard
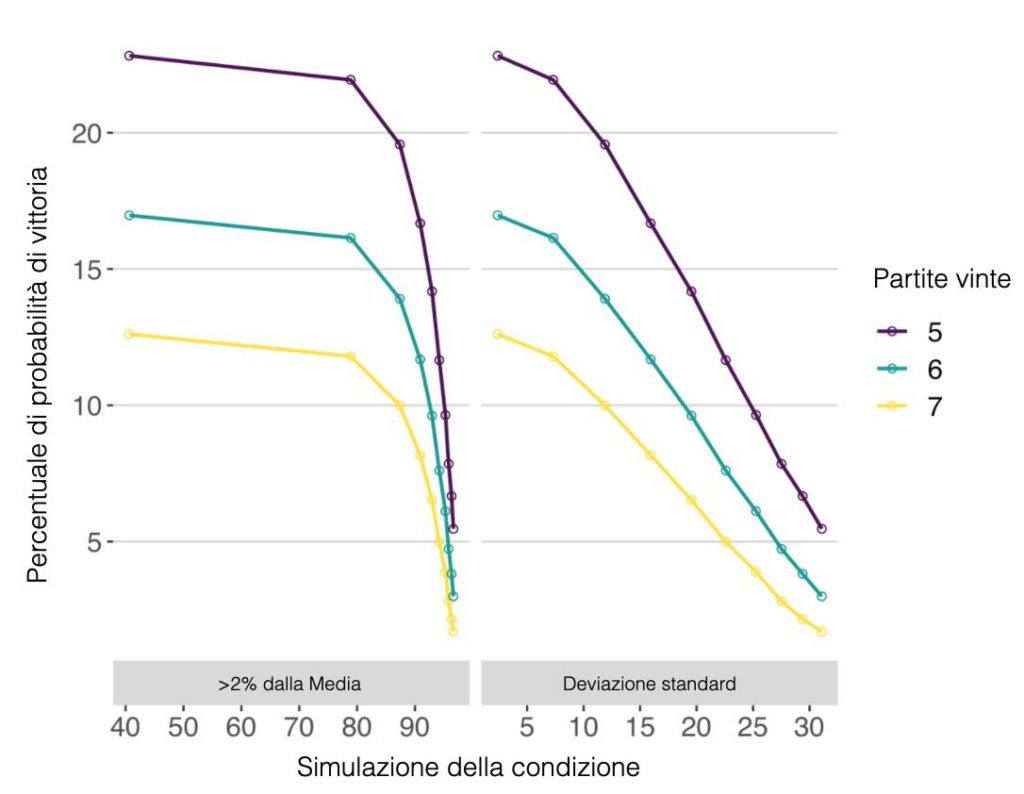
Si tratta, va detto, di condizioni di continuità estreme. Nella realtà, Sabalenka probabilmente si trova in un intervallo dai 10 ai 15 punti percentuali di deviazione standard. Ipotizzando di poter ridurre della metà quella varianza, siamo di fronte a un possibile guadagno di diversi punti percentuali nella sua probabilità complessiva di vittoria. Non è una differenza determinante ma, con solo quattro prove dello Slam all’anno, deve essere tenuta in considerazione.
Questa minima analisi di un aspetto della continuità di gioco mostra che la simulazione di torneo è uno strumento utile per approfondire tematiche relative alla varianza da una partita all’altra. E, in questo senso, ci sono ancora molte domande che meritano un’esplorazione. ◼︎


