Pubblicato il 31 ottobre 2019 su betfair | The Hub – Traduzione di Edoardo Salvati
// A grandi linee, i modelli predittivi nel tennis possono essere raggruppati in tre categorie: quelli basati su sistemi di classifica, quelli di regressione e quelli basati su situazioni di punteggio. Nessuna categoria esclude l’altra, sono anzi tra loro aggregabili, ma le metodologie a cui si riferiscono possiedono elementi distintivi.
Modelli basati su sistemi di classifica
Questo tipo di modelli fanno previsioni sul risultato delle partite quantificando la bravura di ogni giocatore, per poi assegnare al più bravo dei due maggiore probabilità di vittoria. I più semplici e conosciuti sono le classifiche ufficiali ATP e le classifiche ufficiali WTA, che hanno una buona capacità predittiva. Ad esempio, nel 2014 il giocatore con la classifica più alta ha vinto il 68.1% delle partite del circuito maggiore. Esiste però un’alternativa con potere predittivo più alto rispetto a quello delle classifiche ufficiali.
Sto parlando delle valutazioni Elo, che prendono il nome dal loro inventore, Arpad Elo, che le ha originariamente sviluppate per gli scacchi. Le valutazioni Elo assegnano a tutti i giocatori lo stesso punteggio iniziale di 1500, che viene aggiornato dopo ogni partita. Se da una parte le classifiche ufficiali attribuiscono punti ai giocatori in funzione del turno raggiunto e della categoria del torneo, il numero di punti Elo guadagnati o persi dipende dalla valutazione Elo dell’avversario. Se un giocatore ne batte un altro con valutazione Elo superiore, guadagna più punti di quanti ne guadagnerebbe vincendo contro uno con valutazione inferiore alla sua. Invece, se un giocatore perde contro un altro giocatore con una valutazione Elo inferiore, perde più punti di quanti ne perderebbe contro uno con una valutazione superiore.
Inoltre, le valutazioni Elo prevedono una formula per convertire la differenza di punteggio in probabilità di vittoria. Una differenza di 100 punti implica che il favorito ha una probabilità di vittoria del 64%; una differenza di 200 punti implica una probabilità del 76%, una differenza di 300 punti implica una probabilità dell’85%, una differenza di 400 punti implica una probabilità del 91% e una differenza di 500 implica una probabilità del 95%.
L’aspetto che rende così attraenti le valutazioni Elo è l’abilità di produrre previsioni molto accurate. In uno studio di Stephanie Kovalchik sull’analisi di undici modelli predittivi di tennis pubblicamente disponibili, tra cui tutti quelli riportati in questo articolo, le valutazioni Elo sono risultate più precise di qualsiasi altro (con un livello di esattezza del 70% per il circuito maschile nel 2014) a eccezione delle quote scommesse (che hanno raggiunto il 72%).
Modelli di regressione
L’utilità di questi modelli si manifesta in presenza di informazioni disponibili che possono avere valore predittivo di un risultato, ma tra le quali non è nota una precisa correlazione. Ad esempio, un giocatore dalla classifica più alta vincerà probabilmente contro un giocatore più indietro di lui, ma a quale percentuale di probabilità corrisponde, diciamo, una differenza di 10 punti nelle loro classifiche?
Un modello di regressione è in grado di produrre una stima. Date delle variabili predittive del risultato di una partita, il modello valuta se sono effettivamente correlate al risultato e, nel caso lo siano, quantifica la correlazione. Un’analisi di questo tipo è stata fatta dagli autori Julio del Corral e Juan Pietro-Rodriguez in un lavoro del 2010, costruendo un modello con 20 variabili comprensive della differenza di classifica, della fase del torneo (il turno) e del torneo stesso (quale Slam dei quattro esaminati), delle differenze tra giocatori, come il fatto che uno o entrambi fossero mancini o fossero stati tra i primi 10 in passato. Per il circuito maschile, è emerso che la differenza di classifica è l’elemento predittivo più importante. Anche variabili come la differenza di età e i risultati in precedenti edizioni del torneo hanno un ruolo. Altre si sono rilevate invece prive di importanza, come la differenza in altezza.
I modelli di regressione hanno buone prestazioni e sono un valido strumento perché la loro accuratezza dipende in larga misura dalla bontà delle variabili. I migliori tra i modelli a disposizione non sono così precisi come le valutazioni Elo (nel 2014 hanno raggiunto un livello di esattezza del 68% per il circuito maschile), ma potrebbero diventarlo con variabili più puntuali. Inoltre, possono essere usati con grande efficacia per mettere insieme aspetti predittivi di diversi modelli: ad esempio, un modello di regressione basato sulle valutazioni Elo e con variabili aggiuntive sarebbe molto interessante.
Modelli basati su situazioni di punteggio
L’ultima classe di modelli ampiamente utilizzati nel tennis si basa sulle situazioni di punteggio. Mentre le valutazioni Elo sono applicabili a molteplici sport e i modelli di regressione hanno una valenza più generica, i modelli basati sulle situazioni di punteggio sono specificamente pensati avendo a riferimento le regole del tennis. In questo caso l’idea è di provare a creare un modello di una partita di tennis partendo dal singolo punto. Si ipotizza cioè che ogni giocatore ha una probabilità costante di vincere un punto al servizio per tutta la partita. Una volta fatta questa ipotesi, calcolare la probabilità di vincere un game al servizio, un set o l’intera partita si riduce alla sommatoria di tutte le possibili combinazioni di vittoria. La matematica sottostante è decisamente complicata, ma sono poi equazioni velocemente risolvibili tramite computer.
IMMAGINE 1 – Esempio di modello basato su situazioni di punteggio
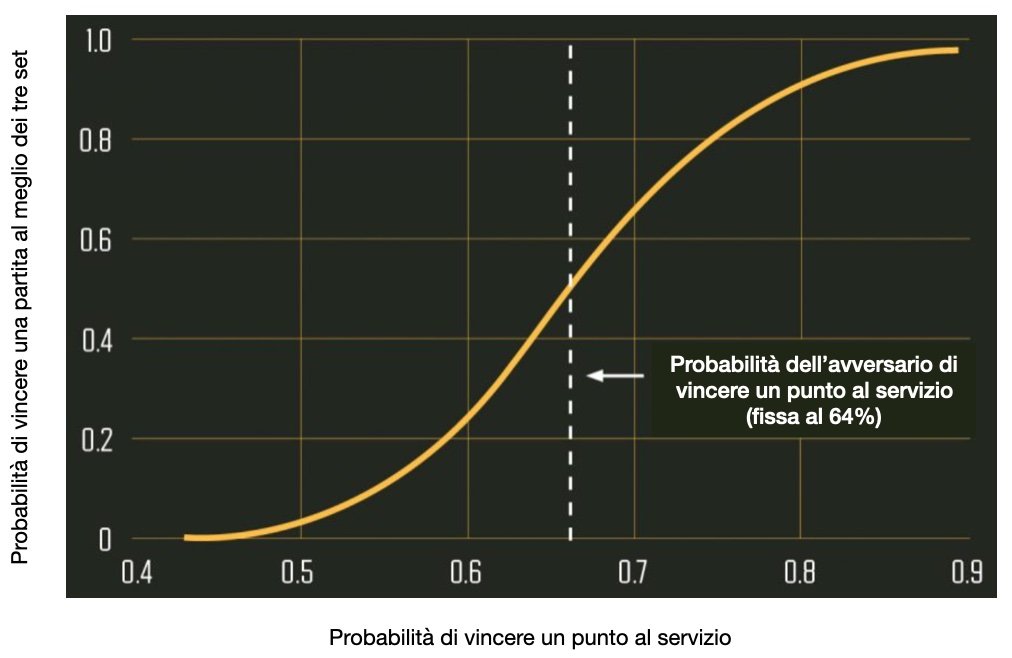
L’immagine 1 è un esempio di applicazione delle equazioni. Fissando la probabilità dell’avversario di vincere un punto al servizio al 64% (la media sul circuito maggiore), è possibile calcolare la probabilità di un giocatore di vincere la partita sulla base di diverse probabilità associate al suo servizio. La linea tratteggiata rappresenta la probabilità dell’avversario di vincere un punto al servizio, pari a 64%. Se anche l’altro giocatore vince il 64% dei punti al servizio, la sua probabilità di vittoria è esattamente del 50%. Se vince il 60% dei punti al servizio però, la probabilità scende al 31%. Se vince il 70%, sale invece al 77%.
Ipotizzare che la probabilità di vincere un punto al servizio sia costante per tutta la durata della partita può sembrare un po’ semplicistico. Significa ad esempio che il modello assegna la stessa probabilità di salvare una palla break in un game del set decisivo come di vincere il primo punto della partita, anche se si presuppone che una palla break eserciti molta più pressione sul giocatore al servizio, influenzando la probabilità di vincerla. Gli autori Franc Klaassen e Jan Magnus hanno analizzato la validità dell’ipotesi. Per quanto i loro risultati la smentiscono, cioè è più probabile che sotto pressione un giocatore al servizio perda il punto, e che aspetti come il vantaggio psicologico rivestono un ruolo, hanno comunque concluso che è una buona approssimazione predittiva.
Se teniamo valido l’assunto di una probabilità costante (spesso indicato anche come l’ipotesi di indipendente e identicamente distribuito, o i.i.d.), la sfida nell’utilizzo di questi modelli è di prevedere con esattezza le probabilità in questione per entrambi i giocatori. Uno degli strumenti più efficaci al riguardo è il modello corretto per avversario degli autori Tristan Barnett e Stephen R. Clarke, che mettendo insieme statistiche sul rendimento — la bravura al servizio e alla risposta rispetto al giocatore medio — elabora stime di percentuale di vittoria al servizio per ogni partita. È un modello che ottiene risultati sull’esito di una partita simili a quelli dei modelli di regressione, buoni ma inferiori a Elo (livello di esattezza del 67% per il circuito maschile).
IMMAGINE 2 – Punteggio di set più probabile nella finale di Wimbledon 2016 se visto per Murray
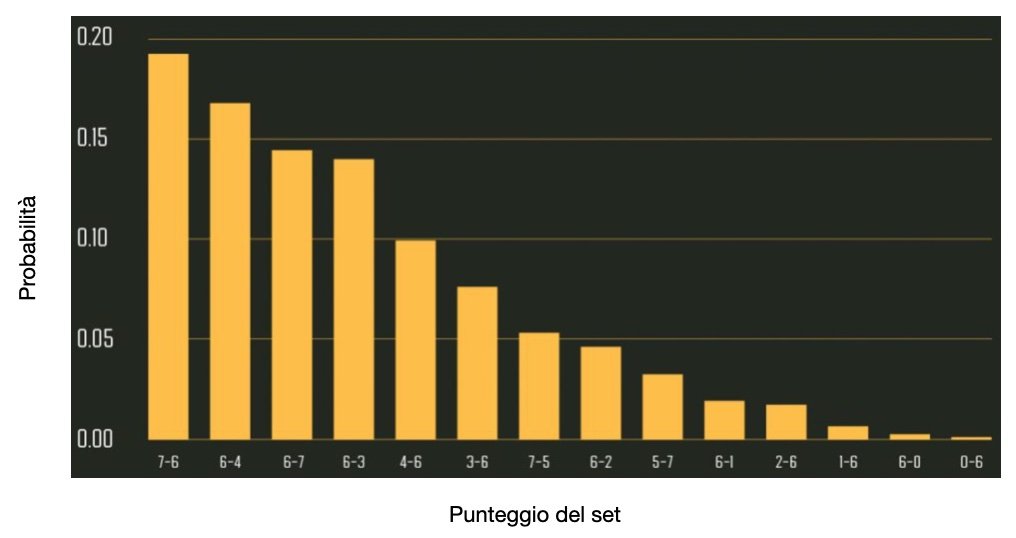
I modelli basati su situazioni di punteggio sono interessanti perché in grado di produrre un numero enorme di informazioni da una singola partita. Visto che l’unità di base è il singolo punto, riescono facilmente a generare probabilità sul numero di set, numero di game e punteggio del set, solo per citarne alcune. A titolo di esempio, l’immagine 2 mostra la previsione di punteggio più probabile per set della finale di Wimbledon 2016 tra Andy Murray e Milos Raonic. Il modello di Barnett & Clarke assegnava il 70.9% di probabilità di vincere il servizio a Murray e il 67.0% a Raonic. Rispetto a queste percentuali e secondo l’ipotesi i.i.d., punteggi di 7-6 e 6-4 erano i più probabili. Il modello si è comportato ottimamente: Murray ha vinto per 6-4 7-6 7-6.
Riepilogo
Ciascuno dei tre modelli con cui il risultato di una partita di tennis può essere pronosticato ha i suoi meriti: la regressione è molto flessibile, le valutazioni Elo sono molto accurate e le situazioni di punteggio forniscono una ricchezza informativa incredibile su ogni partita. ◼︎


