Pubblicato il 14 febbraio 2020 su HiddenGameOfTennis – Traduzione di Edoardo Salvati
// Il capitolo 9 del libro Analyzing Wimbledon di Franc Klaassen e Jan Magnus esamina il compromesso che incombe su qualsiasi giocatore in procinto di servire, tra non sbagliare il servizio e vincere il punto al servizio. In generale, se un giocatore rinuncia a un po’ della potenza o profondità del servizio per aumentare la probabilità di metterlo in campo, si determina un effetto negativo sulla possibile vittoria del punto. Ma è vero anche l’opposto: spingere sul servizio tipicamente riduce la probabilità che il servizio sia valido, ma se rimane in campo, allora ha un effetto positivo sulla possibile vittoria del punto. Da qualche parte tra questi due scenari si posiziona la strategia ottimale di massimizzazione dei punti vinti al servizio.
Per quanto mi riguarda, il capitolo 9 è il più denso di contenuti matematici di tutto il libro. Chi ha familiarità con la statistica potrà non sentirsi spaesato. Per quelli invece come me con una formazione più umanistica, derivate, gamma e lambda sono al limite dell’incomprensione. Gli autori inoltre saltano alcuni passaggi, dando per scontato che il lettore abbia un minimo di preparazione in materia, o perché hanno voluto evitare di eccedere in spiegazioni. Pur avendo letto quel capitolo almeno un centinaio di volte (e non è un’esagerazione!), non ho ancora capito con esattezza il modo in cui il loro modello è stato creato. Ho trovato però il sistema per applicarlo a un’analisi dell’efficienza dei giocatori al servizio.
Di che dati abbiamo bisogno?
Questa è la parte facile. Servono quattro percentuali:
- Prime in campo (1maIn%)
- Punti vinti con la prima (1maPVS%)
- Seconde in campo (2ndaIn%), che non è una statistica comunemente disponibile, ma che si può facilmente derivare da statistiche comunemente disponibili, in particolare la percentuale di doppi falli, solitamente calcolata rispetto al totale dei servizi giocati (e non solo le seconde giocate)
- Punti vinti con la seconda quando la seconda è valida (2ndaPVS%), dato che differisce da quello comunemente indicato di percentuale di punti vinti con la seconda, che invece è calcolato come punti vinti con la seconda diviso per seconde servite (in sostanza, in questo caso si ignorano i doppi falli).
Cosa facciamo con queste quattro percentuali?
L’idea è che la 1maIn% e la 1maPVS% creano un punto (x,y) di una curva, e la 2ndaIn% e la 2ndaPVS% creano un altro punto (x,y) di una curva. L’asse x delle ascisse rappresenta la percentuale di servizi validi, l’asse y delle ordinate la percentuale dei punti vinti al servizio. Il problema è che se si uniscono questi due punti, si ottiene una retta, non una curva, e l’efficacia al servizio non è lineare. Klassen e Magnus hanno quindi sviluppato una funzione che introduce una curva. Per capire come, serve leggere il libro e soffrire diverse emicranie.
Con la loro funzione, si può costruire una curva che parte in alto a sinistra del grafico (dove c’è una bassa percentuale di servizi validi, presumibilmente perché è più difficile servire e rispondere a quel tipo di battute, a cui corrisponde un’alta percentuale di vittoria) e scende lentamente verso il lato destro all’aumentare della percentuale di servizi validi e alla conseguente diminuzione della percentuale di punti vinti al servizio. Chiamiamola curva-y, che determina semplicemente la velocità con cui si verifica il compromesso tra servire in campo e vincere punti al servizio (se ne può vedere una rappresentazione all’immagine 1).
Utilizzando altre funzioni e derivate, gli autori stabiliscono il momento in cui un aumento della 2ndaIn% non comporta più un miglioramento della probabilità di vincere il punto, contribuisce anzi a favorire la probabilità di perdere il punto. Vediamola così: in teoria, si potrebbe servire una seconda in modo che sia sempre in campo. Cosa farebbe però l’avversario di fronte a una seconda così debole? Sarebbe meglio quindi servire una seconda di maggiore penetrazione, sacrificando la percentuale 2ndaIn% a favore della 2ndaPVS%. La funzione di Klaassen e Magnus trova esattamente quello “spartiacque”, che diventa la 2ndaIn% ottimale, da cui poi si può risalire l’asse x sulla curva-y per trovare la corrispondente 2ndaPVS%.
Cosa si può dire della prima? Dopo aver trovato la 2ndaIn% e la 2ndaPVS% ottimali — e dico “l’ottimale” ma, come spiego a breve, dovrei dire “un’ottimale” — si può usare un’altra serie di funzioni e derivate per trovare una 1maIn% ottimale. In sostanza, se si disegna una tangente piatta di una curva (w(x)) con apice nella 2ndaIn% ottimale, e la si prolunga fino a un’altra curva (w’(x)) derivata della curva w(x), si trova una 1maIn% ottimale. Lo so, è complicato, ma non vi preoccupate. Il grafico verso la fine dell’articolo può essere utile per visualizzare il concetto. Comunque, anche qui si risale l’asse x sulla curva-y all’altezza di un’ottimale 1maIn% per trovare la corrispondente 1maPVS%.
Valutazioni di efficienza
Siamo ora in possesso di due coordinate ottimali di riferimento che possono essere usate per un confronto con le coordinate effettive di un giocatore. Detto in altro modo, se si usano quei due punti ottimali per calcolare una percentuale complessiva di punti vinti al servizio (PVS%) — che chiamiamo PVS% ottimale — si può poi confrontarla con la PVS% effettiva del giocatore. Nel libro, i due autori dividono la PVS% effettiva per la PVS% ottimale così da ottenere un valore di efficienza, che teoricamente varrebbe 1 (o il 100%) per un giocatore perfettamente efficiente, ma che in pratica è sempre inferiore.
Klaassen e Magnus non hanno evidenziato l’efficienza di specifici giocatori ma, grazie ai dati di Wimbledon a loro disposizione, hanno determinato un’efficienza complessiva per gli uomini (98.9%) e per le donne (98.0%). Inoltre, hanno mostrato con dei grafici di densità quale percentuale di giocatori e giocatrici è particolarmente inefficiente: ad esempio, il 25% dei giocatori aveva un’inefficienza di più dell’1.4% e il 5% dei giocatori un’inefficienza superiore al 3.3%. Se riuscite a digerire la matematica o se avete voglia di rileggere cento volte, è materiale molto interessante e che suggerisco.
C’è un trucco in tutto questo?
Il trucco è che la funzione che determina la curva-y ha un esponente, che i due autori definiscono lambda. La scelta del valore da assegnare a lambda incide pesantemente sulla forma della curva-y, andando quindi a variare notevolmente le percentuali ottimali di prima e seconda di servizio in campo (In) e di punti vinti, che sono il risultato dell’applicazione delle funzioni.
Qual è il lambda corretto? Non ne ho idea, e penso che non l’avessero nemmeno Klaassen e Magnus. Sono però arrivati alla conclusione che sulla PVS% ottimale complessiva non influisce più di tanto il valore di lambda, così che le valutazioni di efficienza non subiscono variazioni. Sono invece la 1maIn% e la 2ndaIn% ottimali a essere sostanzialmente modificate con un lambda diverso. Questo fa dire agli autori che “si dovrebbe fare attenzione a trarre conclusioni in merito alla strategia ottimane a meno di non avere una stima ragionevole di lambda”.
Purtroppo, non ci sono istruzioni nel libro per calcolare una stima ragionevole di lambda. Klassen e Magnus invece usano 3.07 per gli uomini e 3.83 per le donne. Non c’è indicazione di come siano arrivati a quei valori, o se funzionino anche con un insieme di dati più ampio, su superfici diverse tra loro, in periodi di tempo distanti, etc. Non sono comunque numeri tirati a caso, si presume quindi che gli autori abbiano trovato sufficienti prove perché quei due valori di lambda siano in una relazione sensata con le dinamiche del tennis.
Wawrinka è un giocatore efficiente al servizio?
Perché scelgo Stanislas Wawrinka e non gli ancora più blasonati Roger Federer, Rafael Nadal e Novak Djokovic? Perché loro tre sono così efficienti da rendere i rispettivi grafici poco interessanti. Ci sono molti giocatori ben più inefficienti di Wawrinka, alcuni prevedibili (Benoit Paire), altri meno (Nick Kyrgios). Wawrinka è un buon caso studio perché è molto efficiente, ma con abbastanza margini di miglioramento da far vedere perché le inefficienze hanno importanza.
Quali dati?
Ho preso il rendimento di Wawrinka sul cemento dall’inizio del 2019 fino al 14 febbraio 2020. Queste sono le quattro percentuali di riferimento:
- 1maIn% = 59.2%
- 1maPVS% = 77.5%
- 2ndaIn% = 95.4%
- 2ndaPVS% = 57.2% (ricordiamo che non è la tradizionale percentuale di punti vinti con la seconda, che è calcolata invece sulle seconde giocate. In questo caso la percentuale è 54.6%, ma se la si applica solo alle seconde valide, diventa 54.6% / 954 = 57.2%).
Se ne ricava una PVS% effettiva di 68.2%. La media del circuito sul cemento per, più o meno, i primi 150 nello stesso periodo è di circa 64.5%.
Strategia ottimale ed efficienza
Con un lambda di 3.07, si ottiene una 1maIn% di 61.7%, che corrisponde a una 1maPVS% ottimale di 76.7% e una 2ndaIn% ottimale di 88.0%, che a sua volta porta a una 2ndaPVS% ottimale di 63.1%. Queste coordinate ottimali producono una PVS% ottimale di 68.5%. Dividendo l’effettivo per l’ottimale (68.2% / 68.5%) otteniamo una valutazione di efficienza del 99.4%.
Se un’efficienza del 99.4% vi sembra molto buona, non vi state sbagliando. Dopo tutto, la strategia ottimale in questo caso aumenterebbe la PVS% di Wawrinka di un solo 0.3%. Ma si sente spesso dire: “margini ridotti”! Ipotizziamo che l’avversario di Wawrinka è un giocatore medio sul cemento tra i primi 150, così da avere una PVS% di circa il 64.5%. Inserendo la PVS% effettiva di Wawrinka in un modello Markov con un avversario al 64.5%, la percentuale attesa di vittoria è del 67.4% (per una partita al meglio dei tre set).
Ripetendo il calcolo ma con la PVS% ottimale, che è più alta solo dello 0.3%, la percentuale attesa di vittoria di Wawrinka sale al 68.6%. Si osserva un effetto moltiplicatore. La differenza di 1.2% equivale all’incirca a una vittoria addizionale ogni cento partite. Al momento, nel 2020 una vittoria è valsa a Wawrinka in media quasi 72 mila dollari. Se un’inefficienza così marginale potrebbe valere 72 mila dollari nello spazio di due stagioni di partite, pensiamo a quanto stanno potenzialmente rinunciando i giocatori inefficienti al servizio.
Diamogli un grafico
L’immagine 1 mostra il grafico dell’efficienza al servizio di Wawrinka. Come si vede dalla legenda, la linea rossa rappresenta la curva-y, calcolata sulla base della funzione di Klaassen e Magnus (se sembra un po’ arancione nel grafico è perché si sovrappone alla linea gialla della curva ottimale). Sulla curva-y rossa ci sono due asterischi blu, cioè le coordinate per le percentuali di 1maIn%, 1maPVS% e di 2ndaIn% e 2ndaPVS% effettive.
La linea arancione chiaro che parte in basso a sinistra dell’asse delle ascisse e sale in alto a destra è la curva w(x), quella che inizia ad appiattirsi non appena si oltrepassa il punto di svolta tra mettere servizi in campo e vincere il punto con quei servizi. Il picco di quella curva è all’88.0%, cioè il valore di 2ndaIn% ottimale. Il punto sulla curva-y con x = 88.0% è il 63.1%, rappresentato da un rombo arancione. Si tratta del livello di compromesso ottimale per la seconda di servizio (tenendo sempre a mente la problematica relativa a lambda di cui ho parlato in precedenza). La linea arancione chiaro non è strettamente necessaria, visto che bastano le equazioni per determinare gli altri punti, ma mi è sembrato utile introdurla per illustrare il metodo del libro e seguirne gli stessi grafici.
La linea grigio chiaro che parte dall’asse delle ascisse e finisce in basso a destra è la curva w’(x), o la derivata della curva arancione chiara w(x). Se si traccia una riga orizzontale che dall’asse di destra incontra il punto di massimo della curva w(x) (all’88.0% sull’asse delle ascisse), cioè una linea tangente, si ottiene la 1maIn% ottimale nel punto in cui questa tangente interseca la curva w’(x), che in questo caso è 61.7%. Il punto sulla curva-y dove x = 61.7% è il 76.7%, evidenziato con un rombo arancione.
IMMAGINE 1 – Efficienza al servizio di Wawrinka
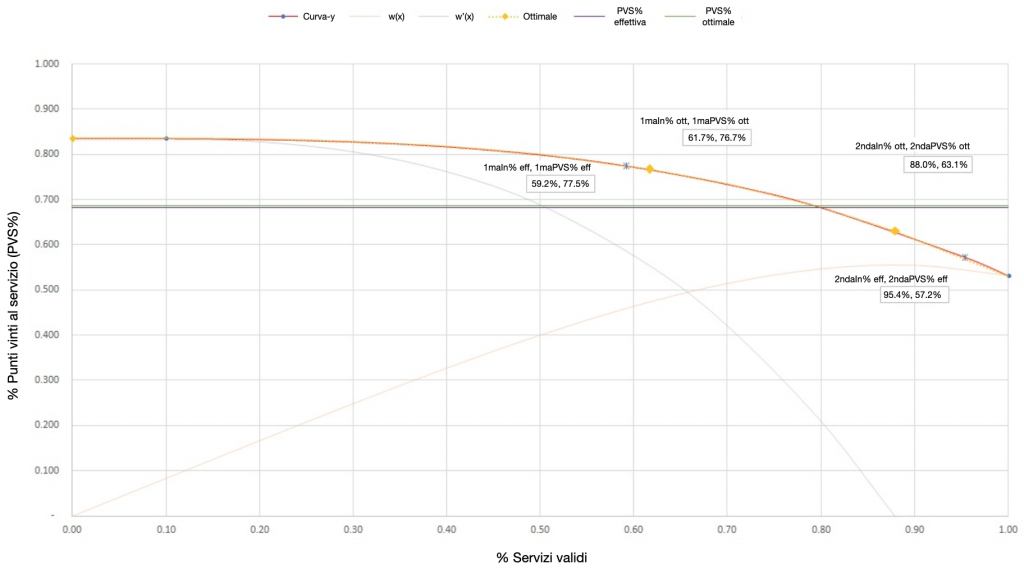
Interpretazione del grafico
Ho creato una linea orizzontale viola scuro che attraversa tutto il grafico, per far vedere la PVS% complessiva effettiva di Wawrinka, e una linea orizzontale verde per far vedere invece la PVS% complessiva ottimale (i colori sono un omaggio al lavoro fatto da Klaassen e Magnus sui dati di Wimbledon). La distanza tra le due linee evidenzia l’inefficienza di Wawrinka. È ridotta, proprio perché abbiamo trovato che Wawrinka ha un’efficienza del 99.4%.
Visto che il valore di lambda è di fatto una stima non perfetta, dobbiamo essere cauti sulla specificità dei rombi arancioni. Potrebbero esserci altre combinazioni di punti sulla curva che definiscono accostamenti di prime e seconde di servizio altrettanto efficienti. Tuttavia, a grandi linee i due autori hanno verificato che il coefficiente lambda non incide più di tanto sulla PVS% ottimale, così che l’analisi sull’efficienza non perde di validità.
Ipotizziamo per un attimo che un lambda di 3.07 è una buona stima di questo campione di dati e che i rombi arancioni abbiano senso. Notiamo che il primo dei due rombi arancioni è alla destra del primo asterisco blu. Questo suggerisce che Wawrinka dovrebbe servire la prima un po’ più lentamente e mettere più prime in campo, con un leggero calo in efficienza. Notiamo però che il secondo rombo arancione è a sinistra del secondo asterisco blu. Questo suggerisce che Wawrinka dovrebbe forzare un po’ di più la seconda — essere quindi meno cauto, vista la bassa frequenza di doppi falli — con un aumento deciso dell’efficienza quando la seconda è in campo.
Altri giocatori
Non posso ovviamente inserire il grafico di ogni giocatore (anche se sono a disposizione di chi volesse chiedermeli). Tutti però vogliono sapere il grado di efficienza di determinati giocatori. Trovate di seguito le valutazioni di efficienza per alcuni dei giocatori e giocatrici più interessanti (almeno a mio avviso), per il periodo 2019-2020 sul cemento.
Uomini
- Djokovic (99.8%)
- Nadal (99.9%)
- Federer (99.8%)
- Thiem (99.3%)
- Medvedev (99.9%) — penso che il dibattito dopo gli US Open 2019 sulla sua strategia al servizio abbia ora fondamento
- Tsitsipas (99.3%)
- Zverev (88.8%) — ahi ahi ahi! Peggiore efficienza maschile dell’analisi
- Isner (96.2%) — sorpreso di un valore così basso, vista la sua reputazione, ma anche ottimi giocatori al servizio possono avere delle inefficienze
- Paire (98.1%) — sorpreso di un valore così alto, immagino che valga la pena fare tanti doppi falli
- Kyrgios (96.1%) — potrebbe migliorare al servizio?
Donne
- Barty (99.2%)
- Halep (99.5%)
- Pliskova (97.6%) — forse è per questo che non ha ancora vinto uno Slam
- Svitolina (99.2%)
- Bencic (99.9%)
- Andreescu (99.9%)
- Kenin (99.8%)
- S. Williams (99.0%) — un po’ sorpreso che non sia più vicino al valore massimo. Pensavo fosse perché sta “invecchiando”, ma anche con i risultati del 2016 non c’è molta differenza
- Osaka (98.5%)
- Kvitova (99.9%)
- Keys (98.3%)
- Sabalenka (100%) — mi viene da sorridere, può sembrare uno scherzo, ma è tutto vero. Non è la perfezione, ma ha la migliore valutazione di efficienza di tutte quelle che ho controllato: 99.963%.
- Muguruza (99.1%)
- Alexandrova (99.0%)
- Kasatkina (99.2%) — in tutta onestà, sbalorditivo. Un altro valido richiamo al fatto che essere bravi al servizio ed essere efficienti non sono la stessa cosa, ma sta facendo del suo meglio.
- Errani — irrisolvibile, e non è una presa in giro. Le funzioni non sono riuscite a creare una soluzione efficiente per Errani. E solo questo può essere una validazione della bontà del modello.
Conclusioni
Alla base di qualsiasi modello ci sono delle ipotesi, e quella più importante in questo caso è il valore di lambda. Per Klaassen e Magnus i due valori di lambda per uomini e donne avevano senso rispetto al campione di dati analizzato, quindi si spera che non siano stime troppo eccentriche. E comunque, sono le migliori che abbiamo. Pur nell’incertezza, con questo modello possiamo misurare l’efficienza complessiva al servizio di un giocatore, perché lambda ha un effetto marginale.
Naturalmente, non è detto che un giocatore sia capace di eliminare un’inefficienza legata al suo servizio, e si parla di un’analisi granulare che non necessariamente ha riscontro nel mondo reale in termini di strategia. Inoltre, se sei perfetto al 99.4% (come Wawrinka), sei già a un livello altissimo. Per giocatori con inefficienze ben più ampie, aggiustamenti nella strategia al servizio potrebbero portare a vantaggi significativi, visto appunto l’effetto moltiplicatore.
Un ringraziamento speciale al sito derivative-calculator.net per avermi sostituito in calcoli che non avrei saputo fare. Grazie al cielo esistono persone intelligenti (e generose). ◼︎


