Le regole proposte da Charles Dodgson per i tornei di tennis

Pubblicato l’1 febbraio 2020 su FreeRangeStatistics – Traduzione di Edoardo Salvati

// In un precedente articolo, ho analizzato l’impatto dell’assegnazione delle teste di serie in un torneo di tennis. Le teste di serie sono uno dei modi per aumentare la probabilità che i giocatori più forti arrivino nelle fasi conclusive di una competizione a eliminazione diretta, portando a esiti più giusti e a maggiori possibilità di riservare gli scontri più entusiasmanti per la fine del torneo. In sostanza, l’obiettivo è ovviare a questo problema:

L’episodio appena descritto portò Charles Dodgson, illustre matematico del diciannovesimo secolo dell’Università di Oxford, a proporre un’alternativa all’allora in voga sistema di eliminazione diretta senza teste di serie. Il suo trattato sul tema dal titolo “ LAWN TENNIS TOURNAMENTS: The True Method of Assigning Prizes with a Proof of the Fallacy of the Present Method” si trova alla pagina 1082 dell’opera omnia. Naturalmente, Dodgson è più conosciuto al mondo come autore a tempo perso di libri per bambini con lo pseudonimo di Lewis Carroll, le cui opere includono il capolavoro “Le avventure di Alice nel paese delle meraviglie”, “ Attraverso lo specchio e quel che Alice vi trovò”, “La caccia allo Snark” e il giustamente dimenticato “Sylvie e Bruno”.

Gli elementi di base

Ecco gli elementi di base del sistema elaborato da Dodgson, descritto per un torneo a 32 giocatori:

• viene tenuto un elenco in cui alla fine di ciascuna partita, accanto a ogni nome si scrive il nome del giocatore o dei giocatori che gli sono stati superiori, o in virtù di una vittoria diretta, o perché hanno battuto qualcuno che a sua volta ci è riuscito (vale a dire se A batte B e B batte C, A e B sono entrambi superiori a C). Non appena accanto al nome di un giocatore ce ne sono altri tre a lui superiori, quel giocatore è cancellato dalla lista

• nella prima giornata di competizioni, c’è solo una partita per giocatore, con i 32 giocatori che sono accoppiati a due a due a formare 16 coppie

• per il secondo giorno […] i 16 giocatori che hanno vinto la prima partita sono accoppiati tra di loro, così come i 16 che hanno un superiore (coloro che perdono in quest’ultimo gruppo di coppie avranno 3 superiori ciascuno, e verranno quindi eliminati dalla lista). Per tutte le altre partite i giocatori sono accoppiati allo stesso modo, prima quelli che non hanno mai perso, poi quelli con un superiore e così via, cercando di evitare, quanto possibile, di accoppiare due giocatori che hanno un superiore in comune

• alla metà del terzo giorno, sono rimasti solo due giocatori senza sconfitte […] e questi due hanno una partita da giocare per tutto il quarto giorno

• alla fine del quarto giorno si conosce il nome del giocatore che ha vinto il primo premio (grazie allo stesso processo di eliminazione usato nel metodo in vigore): i restanti giocatori sono accoppiati secondo le medesime regole, per le due partite da disputare al quinto giorno.

Teoria contro realtà

L’essenza di questo procedimento è che nessun giocatore è eliminato fino a che non è certo che non sia tra i migliori tre, perché gli eliminati hanno almeno tre superiori da cui hanno perso direttamente o che hanno battuto qualcuno che li ha battuti. Così i migliori tre sono in grado di surclassare tutti gli altri.

Un’osservazione interessante è che, secondo le regole di Dodgson, non serve che il numero di giocatori sia in potenza di due, come nel caso di un classico torneo a eliminazione diretta in cui gli organizzatori vogliono evitare situazioni di bye a senso unico.

Dodgson sostiene che la sua proposta dà garanzia di assegnare con accuratezza il primo, secondo e terzo premio ai migliori tre giocatori. Questa si basa però su alcune ipotesi chiave:

• la superiorità è transitiva, quindi se A è superiore a B e B a C, allora A è superiore a C
• la superiorità è deterministica, coerente e costante.

Naturalmente, il mondo reale opera con altri canoni. Ci si interroga quindi sulla bontà del metodo di Dodgson nel momento in cui i risultati delle singole partite non sono costanti e sono incoerenti tra loro, in linea con quanto emerso dalle realistiche simulazioni con valutazioni Elo che ho usato in precedenza. Per scoprirlo, ho simulato tornei impostati secondo le regole di Dodgson con le stesse 128 giocatrici di vertice dal 1990 dei tornei più convenzionali della scorsa analisi. Il codice che ho scritto permette di scegliere l’esito di singoli scontri tra giocatrici, da un lato in senso deterministico (cioè la giocatrice con la valutazione più alta ha garanzia di vincere, come nella dimostrazione a 32 giocatori di Dodgson), dall’altro in senso realisticamente probabilistico (la probabilità di vittoria è casuale, ma legata comunque alla valutazione Elo delle due giocatrici).

Risultati

Se le vincitrici sono deterministici, si arriva a un risultato come quello illustrato da Dodgson

Non deve sorprendere che il suo metodo assegni correttamente i premi in un torneo a 32 giocatori con esiti deterministici delle partite, vista la notevole abilità matematica che possedeva. Ero curioso di vedere se avesse funzionato in presenza di molti più partecipanti, e ho trovato che le sue regole (con modifiche minime) identificano nel giusto ordine i tre giocatori, a cui assegnano i primi tre premi, 100 volte su 100 diverse simulazioni.

Anche un torneo a eliminazione diretta con esito deterministico delle partite e con una corretta attribuzione delle teste di serie farà emergere con precisione le quattro migliori giocatrici il 100% delle volte. Credo che Dodgson pensasse che non si potesse fare affidamento su una conoscenza aprioristica del livello dei giocatori, escludendo quindi la possibilità di un torneo con teste di serie. Di sicuro, l’unico confronto che ha fatto è tra il suo metodo e un tabellone senza teste di serie.

È da notare che nel torneo ipotizzato da Dodgson serviranno all’incirca il doppio delle partite (con variazione a seconda dell’efficienza del tabellone, anche se in media nelle mie simulazioni le partite sono state 240) di un torneo a eliminazione diretta (che ha bisogno di 127 partite per 128 giocatori).

I risultati non sono così puntuali nello scenario in cui le vittorie sono realisticamente probabilistiche

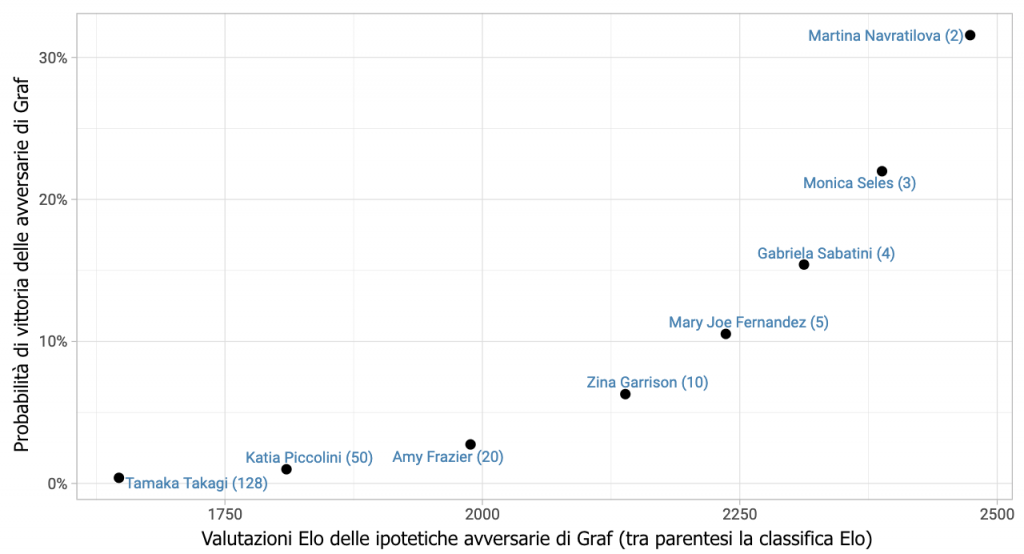
In presenza di esiti non deterministici ma dipendenti dal caso e legati alla differenza di bravura associata alle valutazioni Elo, il metodo di Dodgson non è valido quanto avrebbe sperato. Naturalmente, si tratta sempre di un modello realistico. Anche nel periodo di dominio totale, Steffi Graf (la giocatrice con la valutazione massima tra quelle prese in esame per gli anni ’90) poteva comunque avere qualche probabilità di perdere contro altre giocatrici di vertice in una qualsiasi partita, come visto nel grafico che qui ripropongo.

IMMAGINE 1 – Probabilità di alcune giocatrici tra le prime 128 di battere Graf alla fine del 1990 sulla base delle valutazioni Elo

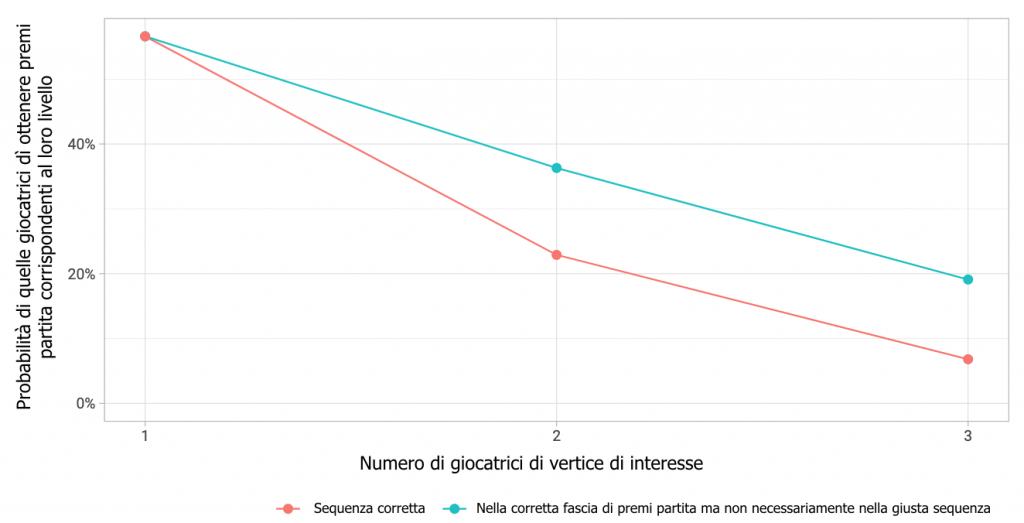
Il grafico dell’immagine 2 mostra i risultati di una simulazione di 1000 tornei giocati secondo le regole di Dodgson, con realistiche probabilità di vittoria e sconfitta (quindi non solo 1 e 0). Alcune conclusioni che si possono derivare:

• le giocatrici di vertice vincono il torneo il 57% delle volte
• il 36% delle volte giocano la finale le prime due giocatrici e il 23% delle volte vince la testa di serie numero 1
• le prime tre giocatrici vincono i primi tre premi partita nell’ordine giusto solo il 7% delle volte.

Nel modello deterministico di Dodgson, per queste tre casistiche la probabilità è del 100%.

IMMAGINE 2 – Rendimento delle regole proposte da Dodgson in termini di probabilità della prima, seconda e terza giocatrice di finire il torneo nella giusta posizione

L’efficacia delle valutazioni Elo

Nel modello probabilistico, gli esiti del torneo secondo le regole di Dodgson sono simili a quelli di uno a eliminazione diretta con teste di serie, come ho scritto in precedenza. Ad esempio, in un tabellone con teste di serie, Graf, la giocatrice più forte, vinceva il 60% dei tornei e le prime due giocatrici erano in finale il 42% delle volte. È un risultato marginalmente migliore, rispetto a quanto ottenuto con le regole di Dodgson, in circa la metà delle partite, a evidenza dell’efficacia dell’utilizzo di informazioni aprioristiche sulla bravura delle giocatrici per la determinazione delle teste di serie.

Attuazione

Metodologia

Applicare le regole di Dodgson in modo che fossero sostenibili su un più ampio campione di tornei, su esiti casuali di partite e su risultati non coerenti e non transitivi è stato tutt’altro che banale.

Alcune decisioni:

• per le coppie iniziali di giocatrici (e gli scontri successivi) ho proceduto casualmente anziché in ordine alfabetico secondo il cognome

• ho abbandonato l’idea di “turno”, concentrandomi invece sulla successiva partita individuale da giocare, mettendo insieme, ove possibile, giocatrici con lo stesso numero di game giocati e di sconfitte

• ho introdotto un concetto di “giocatrice scomoda” per un qualsiasi momento, vale a dire una giocatrice che ha giocato meno game delle altre e ha il minor numero di avversarie legittime disponibili a parità di sconfitte, evitando rivincite, etc. Trovare una partita per la giocatrice scomoda è diventata la priorità in ogni iterazione della mia simulazione

• in alcune circostanze, ho dovuto permettere partite tra giocatrici che avevano giocato, a quella data, un diverso numero di game. Esiste probabilmente una soluzione che non richiede di farlo, ma non ho avuto tempo di cercarla

E ancora:

• non sono riuscito neanche a escogitare un sistema pratico per il requisito “cercando di evitare, quanto possibile, di accoppiare due giocatori che hanno un superiore in comune”. Tranne che per occorrenze insolite, ho escluso le rivincite così da evitare che l’algoritmo si bloccasse

• con risultati non deterministici e consentendo le rivincite dove inevitabile, sono emerse alcune contraddizioni da gestire con cautela. Ad esempio, una giocatrice può diventare superiore a se stessa (se A è battuta da B e poi B è battuta da A in una rivincita, la futura A è ora superiore alla passata A, un caso che ho evitato di considerare nel conteggio)

• è possibile che le ultime quattro giocatrici rimaste abbiano 3 superiori ciascuna come risultante di una singola partita verso la fine del torneo, rendendo il piazzamento non chiaro. Di fronte a questa evenienza, ho suddiviso il primo posto ex-aequo, anche se semifinali e finale sarebbero più realistiche

• allo stesso modo, può succedere che la giocatrice 2 e 3 (delle tre rimanenti) siano eliminate in un solo passaggio. Questo significa nessuna finale e un play-off per definire il secondo posto.

Interessante e valido, ma di difficile adozione

In ogni caso, si è trattato di un esperimento divertente. Sono soddisfatto del buon funzionamento di questo metodo per lo svolgimento di un torneo, anche al costo di dover giocare quasi il doppio delle partite di un torneo a eliminazione diretta. E, tutto sommato, anche con esiti di partite realisticamente incerti e non costanti. Non è ovviamente perfetto come l’ideale mondo deterministico descritto nel trattato originario di Dodgson. Come il precedente elenco di decisioni e insidie mostra, l’analisi però può complicarsi molto facilmente. Ci sono parecchi casi insoliti e al limite su cui non mi sono soffermato in dettaglio.

A mia conoscenza, il metodo di Dodgson non è mai stato usato per determinare il tabellone di un effettivo torneo, anche se ci sono state alcune simulazioni simili a questa. Non sono sicuro di quanto le intenzioni dello stesso Dodgson fossero serie. Sempre nel trattato accenna alla possibilità di eliminare i set nel tennis a favore in un sistema più semplice come “il primo giocatore che vince 14 game, o che va avanti di 9, vince la partita”. Dubito però che si aspettasse ragionevolmente una calorosa accoglienza delle sue proposte. Vale comunque la pena notare che l’autore del trattato è la figura professionale Charles Dodgson, appassionato di matematica ricreativa, e non Lewis Carroll, autore di libri per bambini.

Diciamo che, come per molte altre sue opere, la pubblicazione ha un merito. Non mi sbilancerei però a suggerirne l’adozione integrale per i moderni tornei di tennis. ◼︎

Analysing the effectiveness of tennis tournament seeding