Pubblicato il 3 dicembre 2016 su PrincetonSportsAnalytics – Traduzione di Edoardo Salvati
// Negli ultimi tempi, organizzazioni come la NCAA (la lega collegiale americana) hanno cercato di incrementare l’audience televisiva del tennis introducendo modifiche al regolamento con l’obiettivo di ridurre la lunghezza delle singole partite.
La logica sottostante questi cambiamenti è di aumentare l’importanza relativa di ciascun punto in modo da rendere l’esperienza complessiva più emozionante. Ritengo sia una questione di primaria importanza per uno sport alle prese con un calo degli ascolti (la finale del singolare maschile degli US Open ha totalizzato 1.4 milioni di telespettatori in meno rispetto a quella dell’anno precedente).
Creare maggiore incertezza?
Creare più incertezza è davvero la soluzione migliore per attrarre pubblico televisivo o per accrescere l’emozione generata da una partita di tennis?
Stabilire quali siano esattamente le regole da modificare per consolidare la base di spettatori rischia di essere un compito improbo. Tuttavia, analizzando statisticamente la selezione dei colpi adottata dai giocatori in più partite di più tornei, è possibile a mio avviso elaborare un indice sostitutivo utile nel definire il livello di emozione o d’interesse di una partita e in grado di arricchire la comprensione della problematica.
Intuitivamente, si tratta di una misurazione dello scostamento della distribuzione nella selezione dei colpi rispetto alla distribuzione di colpi attesa.
Altri modelli utilizzano statistiche dipendenti dall’effetto che ogni punto produce sulla partita nel suo insieme. È sicuramente un approccio legittimo, che tenta di descrivere l’emozione in funzione della maggiore incertezza su quale sarà il giocatore a vincere la partita, ma che non è in grado di catturare l’eccitazione legata alla creatività e alla diversa prestazione in campo dei giocatori.
L’eccitazione deriva da giocate fuori dal comune, che hanno un ruolo importante nell’influenzare il giudizio sulla qualità della partita. Gli scambi considerati più belli sono infatti spesso oggetto di video che poi vengono condivisi sui canali social con effetto moltiplicatore (che, incidentalmente, è anche un modo per avvicinare nuovi appassionati al tennis).
Un modello per le giocate fuori dal comune
Definiamo un semplice modello come segue:
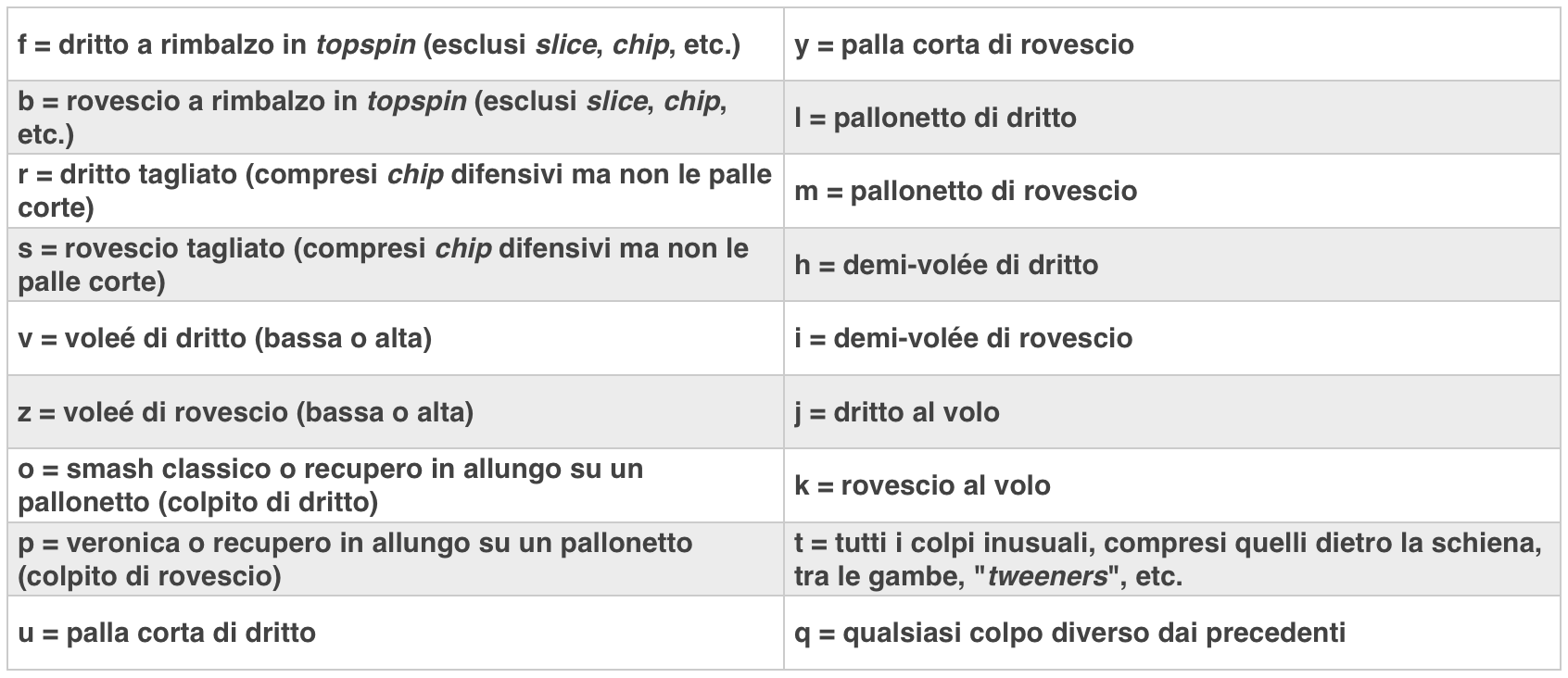
𝐺 è una variabile casuale che assume vettori nella forma
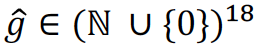
tale che
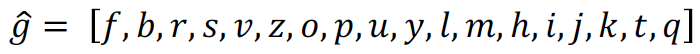
Intuitivamente, si può pensare a 𝐺 come alla rappresentazione numerica di una partita.
Introduciamo una conveniente trasformazione
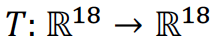
definita come
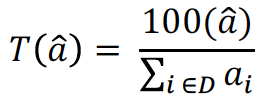
dove D è {1, 2, …, 18} e ai è l’elemento nella i-esima colonna. La trasformazione T converte semplicemente il vettore dei numeri nel vettore delle percentuali. Definiremo una nuova statistica 𝜑 come:
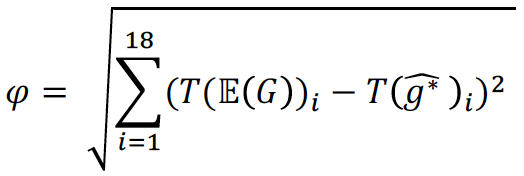
dove
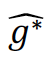
è un’occorrenza osservata di 𝐺.
Valori più alti di 𝜑 danno indicazione di una partita più emozionante (è utile notare che si richiede solo una stima grezza del centro dei dati visto che l’indice in questione restituisce solo informazioni ordinali. In effetti, può andare bene qualsiasi misura del centro). Sviluppando il modello:
𝑇 (𝔼 (𝐺)) = [45.69, 36.16, 2.08, 9.529, 1.384, 1.52, 0.842, 0.057, 0.456, 0.614, 0.403, 0.745, 0.15072, 0.152674, 0.171139, 0.026, 0.015, 0]
𝔼 (𝐺) è stimato dall’insieme di dati a disposizione come
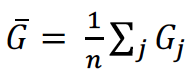
che rappresenta la stima secondo il metodo della massima verosimiglianza per µ di 𝐺, con 𝐺j i vettori casuali indipendenti e identicamente distribuiti con distribuzione di probabilità 𝐺.
Valori campione
La scelta di un vettore partita sulla base di dati reali restituisce i seguenti valori campione:
- 1978 Pepsi Grand Slam – Semifinale – Borg vs Gottfried (6-2 6-4) = 41.5
- 1990 US Open – Finale – Sampras vs Agassi (6-4 6-3 6-2) = 11.21
- 2014 Australian Open – Finale – Wawrinka vs Nadal (6-3 6-2 3-6 6-3) = 9.34
Con più rovesci tagliati di qualsiasi altro colpo, la partita tra Bjorn Borg e Brian Gottfried presenta una deviazione dalla distribuzione standard della selezione dei colpi.
Quella tra Pete Sampras e Andre Agassi si è avvicinata di più al vettore atteso, mostrando tuttavia una deviazione in virtù della volontà di entrambi i giocatori di colpire rovesci a rimbalzo in topspin invece che rovesci tagliati.
La partita tra Stanislas Wawrinka e Rafael Nadal è andata vicino alle aspettative, con solo una percentuale più alta di dritti a rimbalzo in topspin.
Qual è quindi il significato di 𝜑
Da un punto di vista matematico, 𝜑 calcola la distanza tra i due vettori che rappresentano le distribuzioni trovando la norma del vettore differenza (differenza tra il vettore trasformato atteso e il vettore trasformato osservato).
Che tipo di delucidazioni può dare questo valore rispetto a una specifica partita?
In primo luogo, è un valido strumento per identificare quelle partite che si distinguono per la prevalenza di un determinato colpo. Alti valori di 𝜑 possono segnalare dinamiche di gioco atipiche (una prevalenza di volée ad esempio potrebbe indicare scambi più rapidi). Se si necessita di un’analisi più approfondita, si possono studiare gli specifici vettori oggetto di calcolo.
Il vettore trasformato osservato di gioco fornisce la distribuzione della selezione dei colpi durante la partita. La deviazione quadrata di ciascun componente può aiutare a individuare le differenze più significative tra vettore atteso e vettore osservato, utili per trarre conclusioni quantitative relativamente al tipo di colpi giocati e allo stile complessivo della partita.
Pur essendo un indice da cui ricavare molte informazioni, 𝜑 non tiene conto direttamente del posizionamento o della velocità dei colpi, entrambe caratteristiche in grado di incidere sullo stile e sul ritmo di gioco.
Tuttavia, avere maggiore comprensione del tipo di colpi che sono stati usati durante la partita conferisce una solida base statistica da cui dedurre informazioni su velocità e posizionamento.
In media, ad esempio, i colpi tagliati sono più lenti degli smash, e, sempre in media, i pallonetti sono più profondi delle volée. Il valore di 𝜑 può segnalare in quali partite trovare colpi con caratteristiche di velocità o posizionamento più interessanti e valevoli di ulteriore analisi con altre metodologie.
Il fattore sorpresa
Una perplessità che è stata sollevata riguarda la possibilità che alcune partite con alto 𝜑 siano in realtà più noiose di altre con basso 𝜑, aspetto che muoverebbe a sfavore di questa statistica nel catturare le partite interessanti.
Un amico ha portato come esempio una partita fatta solo di dritti, che potrebbe essere più noiosa di una con una classica distribuzione dei colpi. Lo scopo di 𝜑 non è di supportare definizioni soggettive di quanto una partita sia interessante. Sarebbe un approccio per cui è richiesto di identificare un’ideale distribuzione che porta alla “partita in assoluto più interessante”, ma che non è percorribile secondo un metodo davvero basato sulla logica.
Invece, 𝜑 è costantemente in grado di verificare in modo oggettivo lo scostamento dalla norma della modalità in cui è stata giocata una partita. Più è inaspettata, più risulta sorprendente.
E proprio su questo elemento di sorpresa si potrebbe fare leva per attrarre spettatori, visto che è un valore oggettivo da interpretare per classificare quanto una partita sia relativamente interessante. Molto spesso 𝜑 può essere indice di quanto sia emozionante ciascun punto (semplicemente perché non è quello che ci si attende).
Vale la pena sottolineare che l’unica garanzia fornita dal valore 𝜑 𝐺 è che 𝐺 è più irregolare di alcune 𝐺* tale che 𝜑 𝐺* < 𝜑(𝐺). Guarderei comunque con molto interesse anche una partita di soli dritti, ma se si è preoccupati che una partita del genere venga penalizzata per la sua omogeneità, si può introdurre una nuova statistica:
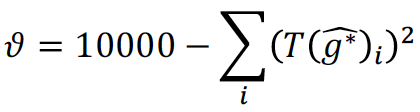
per la quale 𝜗 è massimizzata quando tutte le componenti del vettore partita osservato sono uguali, vale a dire nella partita con la distribuzione di colpi più perfettamente bilanciata.
Esiti positivi
Ritornando al quesito iniziale, possiamo affermare che l’indice 𝜑 sia davvero in grado di riflettere il livello di eccitazione o di interesse che trasmette una partita?
Per certi versi, la risposta è positiva. L’idea di fondo è che eliminando alcuni dei vincoli presenti nel regolamento tennistico del “vincere con (almeno) uno scarto di due” è possibile aumentare le circostanze di un risultato a sorpresa, rendendo le partite a tutti gli effetti più combattute e nel contempo più veloci, ingredienti potenzialmente più accattivanti per conquistare nuovi spettatori.
Parallelamente, partite caratterizzate da un alto valore di 𝜑 avrebbero scambi creativi con colpi poco ortodossi che si presterebbero naturalmente a essere inclusi nei video che circolano sui social e che aiutano ad ampliare la base di spettatori (allo stesso modo in cui spezzoni di giocate memorabili favoriscono l’aumento del numero degli appassionati NBA perché più persone rimangono in estasi di fronte ai tiri impensabili di giocatori come Stephen Curry).
Le partite in cui gli scambi seguono dinamiche meno prevedibili possono essere più interessanti e regalare più emozioni. Sono entrambi aspetti da tenere in attenta considerazione, in ottica di lungo periodo, per migliorare la competizione.
Aumentare l’eccitazione
Allo stesso modo in cui è stato suggerito di eliminare la struttura con vittoria per scarto di almeno due punti nei game ai vantaggi, esiste un modo per incentivare dinamiche di scambio che aumentino il valore 𝜑 di una partita?
Una possibilità sarebbe quella di introdurre qualche tipo di vincolo temporale durante il punto, come ad esempio costringere il giocatore al servizio a provare a terminare lo scambio entro un determinato intervallo di tempo, pena l’assegnazione del punto al giocatore alla risposta (una variazione all’alternanza attacco/difesa del basket).
In questo modo diminuirebbero molti dei dritti o rovesci interlocutori, facendo aumentare di converso i colpi di approccio e i punti a rete. La riduzione dei colpi a rimbalzo si tradurrebbe in un aumento del valore 𝜑 di una partita.
Sarebbe senza dubbio un cambiamento radicale, e quindi di improbabile accadimento, ma sono convinto che per rendere il tennis ancora più emozionante e allargare il numero di tifosi, si dovrebbe valutare – insieme agli altri indici emozionali – anche una statistica come 𝜑, o una della stessa natura. ◼︎


