Pubblicato il 10 giugno 2016 su StatsOnTheT – Traduzione di Edoardo Salvati
// Un’analisi del Mito 13.
Due storie diverse, ma affascinanti in egual misura, sono emerse dal Roland Garros 2016. In campo femminile, la ventiduenne Garbine Muguruza – una stella nascente con una sola precedente apparizione in una finale Slam – ha battuto Serena Williams, conquistando il suo primo Slam in carriera.
Tra gli uomini invece, dopo tre finali perse, Novak Djokovic ha sconfitto Andy Murray per vincere anche lui il suo primo Roland Garros, completando il Grande Slam in carriera e consolidando la sua posizione nel dibattito tra i più grandi di sempre.
Anche se per percorso e contesto le due vittorie sono state molto diverse tra loro – in un caso un gigante del tennis che cerca di imporsi da campione su tutte le superfici, nell’altro una giocatrice che affronta una gigante del tennis che cerca di riscrivere la storia – entrambi i protagonisti hanno dovuto trovare un modo per surclassare due avversari tenaci. Dominare al servizio è stato l’elemento chiave: Djokovic ha vinto il 63% dei punti al servizio contro il 51% dei punti vinti da Murray. Muguruza ha vinto un notevole 62% di punti al servizio contro il 57% di Williams.
Sebbene queste statistiche evidenzino che i vincitori del Roland Garros 2016 sono stati più efficaci al servizio, possiamo dire che sono stati anche più efficienti dei loro avversari? E cosa vuol dire esattamente essere “efficiente” al servizio?
Questo è il tema su cui si concentrano Klaassen e Magnus nel Mito 14 di Analyzing Wimbledon.
Mito 14: ”I giocatori hanno una strategia efficiente al servizio”
Prima di affrontare l’argomento, è necessario soffermarsi sul rapporto rischio-rendimento associato al servizio, il quale si traduce concretamente nell’opposizione tra la probabilità che un servizio sia in gioco e la difficoltà che incontra il giocatore in risposta a ribatterlo. Tutti hanno sicuramente assistito al doppio fallo di un giocatore dovuto a quello che si ritiene un eccesso di spinta sulla seconda. Questo è il rapporto rischio-rendimento in azione.
Come un lanciatore nel baseball o un tiratore nel basket, un giocatore di tennis di vertice deve riuscire a trovare il giusto equilibrio tra la difficoltà e il rischio di un colpo in modo da garantirsi le maggiori probabilità di esito positivo.
La curva-y
Per trovare il punto d’impatto perfetto, Klaassen e Magnus hanno introdotto la “curva-y”, che descrive la relazione matematica tra la probabilità del giocatore al servizio di vincere un punto quando il servizio è in gioco rispetto al rischio che il servizio non sia valido. In altre parole, la “curva-y” è la rappresentazione del rapporto rischio-rendimento.
L’immagine 1 mostra un esempio ipotetico, nel quale si suppone che i servizi più efficaci siano anche quelli a maggior rischio di fallo.
IMMAGINE 1 – Rapporto rischio-rendimento al servizio
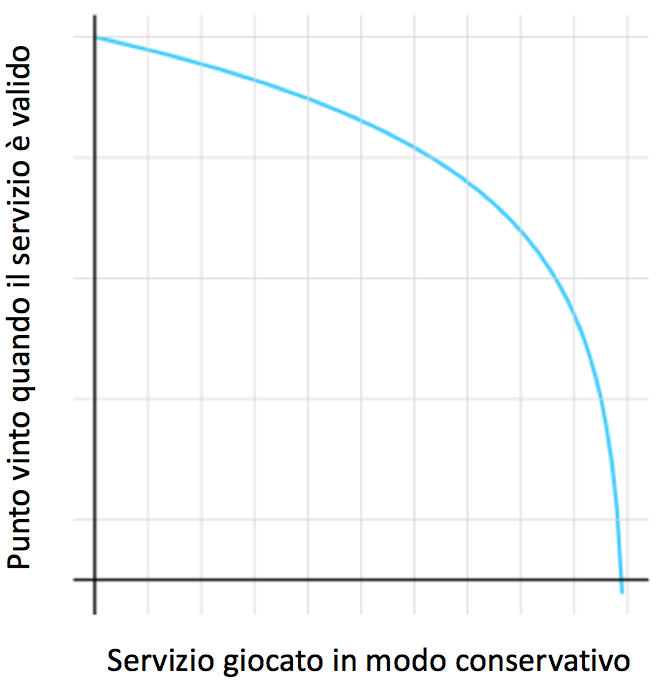
Se la si conoscesse, la “curva-y” sarebbe entusiasmante perché fornirebbe uno strumento utile per trovare la strategia ottimale di un giocatore al servizio. In generale, la strategia ottimale per un giocatore al servizio è quella di giocare per incrementare la probabilità complessiva di vincere un punto. Per vedere come la “curva-y” dell’immagine 1 sia di aiuto nel trovare la strategia ottimale al servizio, il caso più facile da considerare è quello in cui il giocatore al servizio può servire solo la prima. Viene cioè eliminata la seconda di servizio.
Formule
In un tennis con un solo servizio a disposizione, la probabilità di vincere un punto può essere espressa da questa probabilità condizionale:
P(Vittoria) = P(Servizio valido) × P(Vittoria | Servizio valido)
La probabilità di vincere un punto al servizio è data dalla probabilità condizionale di vincere il punto dopo aver servito un servizio valido. Queste due componenti descrivono esattamente la “curva-y”.
È possibile quindi ridurre il problema al calcolo di un solo parametro (cioè servire un servizio valido), sostituendo la probabilità di vittoria quando un servizio è valido con la “curva-y”. Se si riesce in questo, si tratta poi solo di fare una piccola differenziazione per trovare il livello di rischio che massimizza la probabilità di vincere il punto. Questo ci permetterebbe anche di definire “efficiente” il giocatore al servizio che segue una strategia ottimale.
Matematicamente, se si usa il simbolo “*” per rappresentare la migliore percentuale possibile (ottimale) di punti vinti al servizio, si ottiene:
Efficienza = P(Vittoria) / P(Vittoria)*
Per avere il massimo rendimento dal servizio, qualsiasi giocatore vorrebbe un risultato della formula il più possibile vicino a 1.
Stimare l’efficienza al servizio
Due aspetti rendono complicato lo studio della strategia ottimale al servizio. Da un lato, ci sono due servizi nel tennis. Dall’altro, non sappiamo come si presenti la “curva-y”. Il primo problema si risolve abbastanza velocemente estendendo il caso illustrato in precedenza alla situazione di doppio servizio.
Il secondo problema è più complesso da affrontare. Se volessimo veramente conoscere la “curva-y” di un giocatore al servizio (e ipotizzo che la curva rischio-rendimento di ciascun giocatore abbia una forma leggermente diversa), dovremmo fare un esperimento per raccogliere i dati necessari alla sua costruzione: il giocatore al servizio dovrebbe servire indicando all’avversario, per ogni servizio, le sue intenzioni (“Tiro forte e centrale” o “Tiro esterno con molto effetto”, etc), in modo da accumulare molte osservazioni sulla stessa tipologia di servizio, registrare quanto spesso il servizio è valido e quante volte il punto è stato poi vinto contro quell’avversario.
Distribuzione a legge di potenza
In assenza di un esperimento di questo tipo, Klaassen e Magnus hanno preso in considerazione un numero di curve ipotetiche utilizzando una distribuzione a legge di potenza. Hanno poi definito la percentuale di punti vinti e la percentuale di prime di servizio valide come un punto, e gli stessi numeri sulle seconde di servizio come un altro punto. In questo modo sono stati in grado di identificare tutti i parametri della curva ad eccezione della forma. Anche se può sembrare un elemento fondamentale, i due autori non considerano la forma così importante per definire l’efficienza di un giocatore, perché la massima probabilità di vincere un punto al servizio non subisce grossi cambiamenti anche in presenza di grandi variazioni nel parametro forma.
Pur con delle riserve, prendiamo per valido l’approccio di Klaassen e Magnus. Cosa hanno trovato?
Utilizzando le medie osservate (sui servizi validi e sui punti vinti al servizio) sulla prima e sulla seconda di servizio, hanno concluso che l’efficienza al servizio sul circuito maschile è del 98.9%, mentre è del 98.0% sul circuito femminile. Da cui hanno tratto che: “C’è un efficienza molto alta, ma non è un’efficienza totale, quindi rigettiamo l’ipotesi”.
Una rivisitazione dell’efficienza al servizio
Se applichiamo la stessa metodologia al tennis moderno, otterremmo la seguente “curva-y” per gli uomini:
Prob (Vittoria | x) = γ0 − γ1 × x3
e una curva simile per le donne,
Prob (Vittoria | x) = γ0 − γ1 × x3.8
In entrambi i casi, il valore x è la proporzione dei servizi validi, che si pone a complemento del rischio del servizio. Una volta definite le due funzioni, è possibile ottimizzare la probabilità di vincere un punto al servizio per un giocatore o una giocatrice, rispetto alle caratteristiche della loro prima e seconda di servizio. Prendendo come campione tutte le partite giocate dal 2012 al 2014, possiamo confrontare le risultanze di questo metodo di pensiero sulla strategia ottimale di servizio rispetto all’efficienza al servizio dei giocatori di vertice.
Uomini
L’immagine 2 mostra che l’efficienza media per il circuito maschile è del 98% (nella versione originale è possibile visualizzare i nomi dei singoli giocatori puntando il mouse sul grafico, n.d.t.). È un dato perfettamente in linea con quanto calcolato da Klaassen e Magnus e che porta alla stessa conclusione, per cui la maggior parte dei giocatori è inefficiente al servizio di uno o due punti percentuali sulla prestazione ottimale.
IMMAGINE 2 – Efficienza al servizio nel circuito maschile
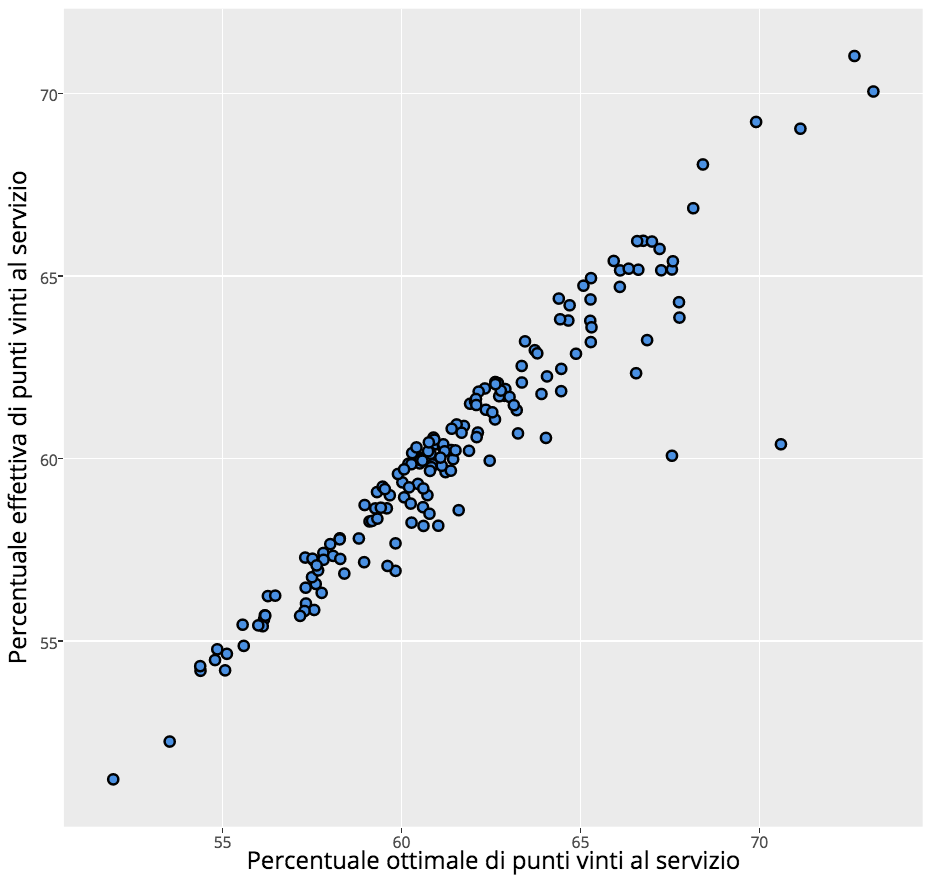
Donne
L’immagine 3 mostra che l’efficienza media per il circuito femminile basata sulle partite dal 2012 al 2014 è stata del 97%, che, seppur di un punto percentuale, è più bassa di quella maschile da una strategia ottimale al servizio.
È interessante notare che un estremo è rappresentato da Victoria Azarenka la quale, secondo l’analisi di Klaassen e Magnus, è più lontana dalla sua percentuale ottimale di punti vinti al servizio rispetto ad altre giocatrici. Azarenka ha una percentuale attesa ottimale di punti vinti al servizio del 69.5% (anche più alta di quella di Williams!), mentre la sua percentuale effettiva nel periodo di riferimento è stata solo del 54%. Naturalmente, questo potrebbe voler anche dire che la media “curva-y” non è una buona rappresentazione dell’efficienza al servizio di Azarenka.
IMMAGINE 3 – Efficienza al servizio nel circuito femminile
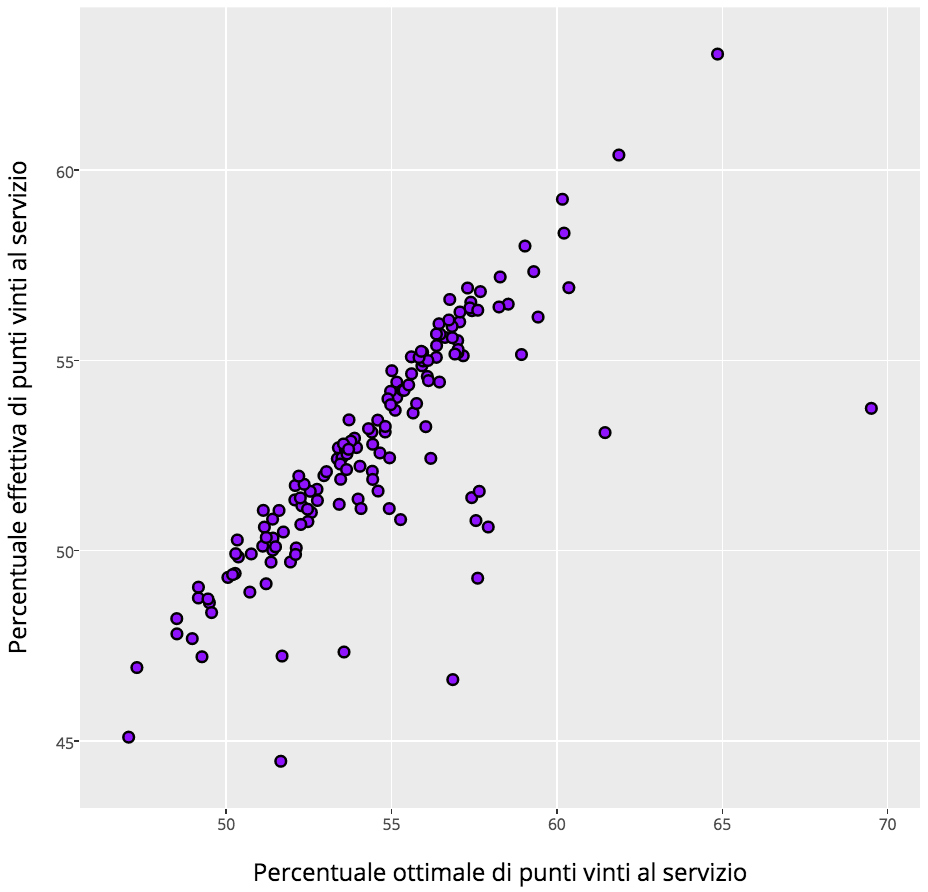
Riepilogo
Il Mito 14 fornisce spunti di riflessione su come provare a costruire un modello che cerchi di rappresentare la strategia ottimale al servizio. Per quanto i due autori presentino risultati interessanti a dimostrazione del fatto che, generalmente, i giocatori non utilizzino una strategia di servizio ottimale – coerentemente ad esempio con altri studi che suggeriscono come i giocatori siano troppo conservativi sulla seconda di servizio – rimane un alone di magia sul modo in cui è stata elaborata la curva rischio-rendimento.
Se si riuscisse a trovare una stima più diretta della curva rischio-rendimento per i singoli giocatori, sarebbe un passo avanti estremamente significativo per la definizione della strategia ottimale al servizio. ◼︎


